Chapter 2 Modelización de la Frecuencia

Resumen del capítulo. Uno de los objetivos primordiales de las aseguradoras es estimar la magnitud de las pérdidas agregadas que debe soportar en virtud de sus contratos de seguro. Las pérdidas agregadas se ven afectadas tanto por la frecuencia de los eventos asegurados como por la cuantía del evento asegurado. Descomponer las pérdidas agregadas en estos dos componentes, cada uno de los cuales requiere una gran atención, es fundamental para el análisis y tarificación. En este capítulo se examinan las distribuciones de frecuencia, las medidas resumen y las técnicas de estimación de los parámetros.

En la Sección 2.1, presentamos la terminología y discutimos las razones por las que estudiamos la frecuencia y la cuantía por separado. Los fundamentos de las distribuciones y medidas de frecuencia se presentan en la Sección 2.2 junto con tres de las principales distribuciones: binomial, Poisson, y binomial negativa. Estas tres distribuciones son miembros de lo que se conoce como la clase de distribuciones (a,b,0), una característica distintiva e identificadora que permite un cálculo eficiente de las probabilidades, que se discute con más detalle en la Sección 2.3. Cuando se ajusta una distribución a un conjunto de datos, es necesario estimar los valores de los parámetros y en la Sección 2.4, se explica el procedimiento para la estimación por máxima verosimilitud. En el caso de los datos de seguros, la observación de 0, que indica la ocurrencia de cero de un evento concreto, es frecuente y puede merecer una atención adicional. Según el tipo de datos, y explicado con más detalle en la Sección 2.5, puede ser imposible tener un cero del suceso estudiado, o la probabilidad de cero puede ser de tal magnitud que el ajuste directo llevaría a estimaciones inadecuadas. Las técnicas de truncamiento o modificación del cero permiten un mejor ajuste de la distribución. Cabe señalar que nuestra cartera de seguros podría estar compuesta por diferentes subgrupos, cada uno con su propio conjunto de características individuales, la Sección 2.6 introduce las distribuciones mixtas y la metodología para permitir esta heterogeneidad dentro de una cartera. La Sección 2.7 describe la bondad de ajuste que mide la razonabilidad de las estimaciones de los parámetros. Los ejercicios se presentan en la Sección 2.8 and la Sección 2.9.1 concluye el capítulo con el código R para los gráficos mostrados en la Sección 2.4.

2.1 Distribuciones de Frecuencias

---

En esta sección se aprende a analizar la importancia de la modelización de las frecuencias en términos

• contractuales,
• de comportamiento,
• bases de datos y
• razones administrativas/regulatorias.

---

2.1.1 Cómo la frecuencia incrementa la información sobre la cuantía

2.1.1.1 Terminología básica

En este capítulo, pérdida, también llamada daño económico, denota la cantidad sufrida por el asegurado. Denominamos siniestro para indicar la indemnización cuando ocurre un evento asegurado, por lo tanto, la cantidad que paga el asegurador. Aunque algunos textos utilizan pérdida y siniestro indistintamente, hacemos aquí una distinción para remarcar cómo las disposiciones contractuales de los seguros, tales como las deducciones y los límites, afectan a la cuantía de la reclamación derivada de una pérdida. La frecuencia representa la frecuencia con la que ocurre un evento asegurado, normalmente dentro de un contrato de póliza. Aquí nos centramos en las variables aleatorias de recuento que representan el número de siniestros, es decir, la frecuencia con la que se produce un evento. La cuantía indica la cantidad, o tamaño, de cada pago de un evento asegurado. En futuros capítulos, se examina el modelo agregado, que combina modelos de frecuencia con modelos de cuantía o severidad.

2.1.1.2 La importancia de la Frecuencia

Recordemos en el Capítulo 1 que fijar el precio de un producto de seguro puede ser un problema complejo. En la fabricación, el coste de un producto es (relativamente) conocido. En otras áreas de servicios financieros, se dispone de precios de mercado. En los seguros, podemos generalizar la fijación de precios de la siguiente manera: empezar con un coste esperado. Añadir “márgenes” para tener en cuenta el riesgo del producto, los gastos incurridos en el mantenimiento del producto y una asignación de beneficios/superávit para el asegurador.

Ese coste esperado para el seguro puede definirse como el número esperado de siniestros por la cantidad esperada por siniestro, es decir, la frecuencia por cuantía esperada. Centrarse en el recuento de siniestros permite al asegurador considerar aquellos factores que afectan directamente a la ocurrencia de una pérdida, generando así potencialmente un siniestro. El proceso de la frecuencia puede entonces modelizarse.

2.1.1.3 Por qué Examinar la Información de la Frecuencia

Las aseguradoras y otros interesados, incluidas las organizaciones gubernamentales, tienen diferentes motivos para generar y mantener bases de datos de frecuencias.

• Contractual. En los contratos de seguro, es común que se enumeren e invoquen deducibles y límites de póliza particulares para cada ocurrencia de un evento asegurado. En consecuencia, los datos de recuento de siniestros generados indicarían el número de siniestros que cumplen esos criterios, ofreciendo una medida única de la frecuencia de los mismos. Por otra parte, los modelos de pérdidas totales aseguradas tendrían que contabilizar los deducibles y los límites de la póliza para cada evento asegurado.

• Conducta. Al considerar los factores que influyen en la frecuencia de las pérdidas, se debería tener en cuenta el comportamiento de riesgo y de su reducción por parte de los individuos y las empresas. Las variables explicativas (de tarificación) pueden tener diferentes efectos en los modelos de la frecuencia de un evento en contraste con el tamaño del mismo.

  • En los seguros de salud, la decisión de utilizar los servicios sanitarios por parte de los individuos, y de reducir al mínimo su utilización mediante medidas de prevención y salud, está relacionada principalmente con sus características personales. El coste por usuario viene determinado por esas características personales, el estado de salud del asegurado, los posibles tratamientos y las decisiones tomadas por el proveedor de atención médica (como el médico) y el paciente. Si bien hay una superposición de esos factores y la forma en que afectan a los costes totales de la atención sanitaria, nos podemos centrar por separado en los factores que afectan la frecuencia de las visitas a los servicios sanitarios y la cuantía de los costes de la atención médica.

  • En productos de seguros a particulares, el historial de siniestralidad es un importante factor de suscripción. Es común utilizar un indicador de si el asegurado tuvo o no un siniestro dentro de un determinado período de tiempo antes del contrato. Además, el número de siniestros incurridos por el asegurado en períodos anteriores tiene capacidad predictiva.

  • En el seguro del hogar, al modelizar la frecuencia de pérdidas potenciales, el asegurador podría considerar las medidas de prevención de pérdidas que el propietario ha adoptado, como los sistemas de alarma o de seguridad visibles. Por otra parte, al modelizar la cuantía de las pérdidas, el asegurador examinaría los factores que afectan a los costes de reparación y sustitución.

• Bases de datos. Las aseguradoras pueden mantener bases de datos separadas que ayudan a desarrollar modelos separados de frecuencia y cuantía. Por ejemplo, un archivo de titulares de pólizas se genera cuando se suscribe una póliza. En este archivo se registra mucha información de suscripción sobre el asegurado o los asegurados, como la edad, el sexo y la información previa sobre siniestralidad; información sobre la póliza como la cobertura, los deducibles y las limitaciones, así como la existencia de reclamaciones de seguro. Un archivo separado, conocido como el archivo de “siniestros”, registra los detalles de la reclamación contra el asegurador, incluyendo la cantidad. (También puede haber un archivo de “pagos” que registra el proceso de los pagos, aunque no nos ocuparemos de eso aquí). Este proceso de recogida de información podría luego extenderse a la modelización por parte de los asegurados como procesos separados de la frecuencia y la cuantía.

• Regulación y Administración. El seguro es una industria altamente regulada y supervisada, dada su importancia en la provisión de seguridad financiera a los individuos y empresas que se enfrentan a los riesgos. Como parte de sus obligaciones los reguladores exigen habitualmente que se informe sobre el número de reclamaciones y las cantidades. Esto puede deberse a que puede haber definiciones alternativas de “cuantía”, por ejemplo, lo pagado frente a lo incurrido, y hay menos posibilidades de error al informar del número de reclamaciones. Esta vigilancia continua ayuda a garantizar la estabilidad financiera de estas compañías de seguros.

2.2 Distribuciones de Frecuencias Elementales

---

En esta sección, aprenderás a:

• Determinar los valores que resumen una distribución como la función de distribución y de supervivencia, así como los momentos como la media y la varianza
• Definir y calcular las funciones generadoras de momentos y de probabilidades
• Describir y comprender las relaciones entre tres importantes distribuciones: binomial, Poisson y binomial negativa

---

En esta sección, presentaremos las distribuciones que se utilizan frecuentemente en la práctica actuarial para modelizar los datos de recuento. La variable aleatoria del número de siniestros se denota con \(N\); por su propia naturaleza toma sólo valores enteros no negativos. Por lo tanto, las distribuciones que se muestran a continuación son todas distribuciones discretas con soporte el conjunto de números enteros no negativos \(\{0, 1, \ldots \}\).

2.2.1 Fundamentos

Dado que \(N\) es una variable aleatoria discreta que toma valores en \(\{0, 1, \ldots \}\), la descripción completa más natural de su distribución es a través de la especificación de las probabilidades con las que asume cada uno de los valores enteros no negativos. Esto nos lleva al concepto de la función de masa de probabilidad (pmf, según sus siglas en inglés) de \(N\), denotada como \(p_N(\cdot)\) y definida de la siguiente manera:

\[\begin{equation} p_N(k)=\Pr(N=k), \quad \hbox{for } k=0,1,\ldots \end{equation}\]

Cabe señalar que hay descripciones completas, o caracterizaciones, alternativas de la distribución de \(N\); por ejemplo, una de ellas es la función de distribución de \(N\) denotada por \(F_N(\cdot)\) y definida a continuación:

\[\begin{equation} F_N(x):=\begin{cases} \sum\limits_{k=0}^{\lfloor x \rfloor } \Pr(N=k), &x\geq 0;\\ 0, & \hbox{en otro caso}. \end{cases} \end{equation}\]

En lo anterior, \(\lfloor \cdot \rfloor\) indica la función entero; \(\lfloor x \rfloor\) indica el mayor entero menor o igual a \(x\). Cabe señalar que la función de supervivencia de \(N\), denotada como \(S_N(\cdot)\), se define como la complementaria de \(F_N(\cdot)\), i.e. \(S_N(\cdot):=1-F_N(\cdot)\). Claramente, esta última es otra caracterización de la distribución de \(N\).

A menudo se está interesado en cuantificar un aspecto concreto de la distribución y no su descripción completa. Esto es particularmente útil cuando se comparan distribuciones. La posición central de la distribución es uno de esos aspectos, y hay muchas medidas diferentes que se utilizan frecuentemente para cuantificarlo. De éstas, la media es la más popular; la media de \(N\), denotada por \(\mu_N\),² se define como

\[\begin{equation} \mu_N=\sum_{k=0}^\infty k~p_N(k). \end{equation}\]

Cabe señalar que \(\mu_N\) es el valor esperado de la variable aleatoria \(N\), i.e. \(\mu_N=\mathrm{E}[N]\). Esto nos lleva a una clase general de medidas, los momentos de la distribución; el momento \(r\)-ésimo de \(N\), para \(r> 0\), se define como \(\mathrm{E}{[N^r]}\) y se denota \(\mu_N'(r)\). Por lo tanto, para \(r>0\), tenemos

\[\begin{equation} \mu_N'(r)= \mathrm{E}{[N^r]}= \sum_{k=0}^\infty k^r~p_N(k). \end{equation}\]

Nótese que \(\mu_N'(\cdot)\) es una función no decreciente bien definida que toma los valores en \([0,\infty]\), como \(\Pr(N\in\{0, 1, \ldots \})=1\); también, nótese que \(\mu_N=\mu_N'(1)\). A partir de aquí, cuando nos refiramos a un momento estará implícito que es finito a menos que se mencione lo contrario.

Otro aspecto fundamental de una distribución es su dispersión, y de las diversas medidas de dispersión estudiadas en la literatura, la desviación estándar es la más popular. Para definirla, primero definimos la varianza de \(N\), denotada por \(\mathrm{Var}[N]\), como \(\mathrm{Var}[N]:=\mathrm{E}{[(N-\mu_N)^2]}\) cuando \(\mu_N\) es finita. Por las propiedades básicas del valor esperado de una variable aleatoria, vemos que \(\mathrm{Var}[N]:=\mathrm{E}[N^2]-[\mathrm{E}(N)]^2\). La desviación estándar de \(N\), denotada por \(\sigma_N\), se define como la raíz cuadrada de \(\mathrm{Var}~N\). Nótese que esta última queda bien definida como \(\mathrm{Var}[N]\), por su definición de promedio de la desviación respecto a la media al cuadrado, y es no negativa; \(\mathrm{Var}[N]\) se denota como \(\sigma_N^2\). Obsérvese que estas dos medidas toman valores en \([0,\infty]\).

2.2.2 Funciones Generadoras de Momentos y de Probabilidad

Ahora presentaremos dos funciones generadoras que son útiles cuando se trabaja con variables de recuento. Recordemos que para una variable aleatoria discreta, la la función generadora de momentos (mgf, según sus siglas en inglés) de \(N\), denotada como \(M_N(\cdot)\), se define como

\[ M_N(t) = \mathrm{E}~{[e^{tN}]} = \sum^{\infty}_{k=0} ~e^{tk}~ p_N(k), \quad t\in \mathbb{R}. \]

Obsérvese que mientras \(M_N(\cdot)\) está bien definida ya que es el valor esperado de una variable aleatoria no negativa (\(e^{tN}\)), aunque puede tomar el valor \(\infty\). Nótese que para una variable aleatoria de recuento, \(M_N(\cdot)\) tiene un valor finito en \((-\infty,0]\) con \(M_N(0)=1\). El siguiente teorema, cuya demostración se encuentra en (Billingsley 2008) (pages 285-6), justifica su nombre.

Theorem 2.1 Consideremos que \(N\) es una variable aleatoria de recuento tal que \(\mathrm{E}~{[e^{t^\ast N}]}\) es finita para algún \(t^\ast>0\). Se tiene lo siguiente:

Todos los momentos de \(N\) son finitos, i.e. \[ \mathrm{E}{[N^r]}<\infty, \quad r \gt 0. \] La mgf se puede usar para generar sus momentos de la siguiente forma: \[ \left.\frac{{\rm d}^m}{{\rm d}t^m} M_N(t)\right\vert_{t=0}=\mathrm{E}{N^m}, \quad m\geq 1. \] La mgf \(M_N(\cdot)\) caracteriza la distribución; en otras palabras, especifica de manera única la distribución.

Otro motivo por el que la mgf es muy útil como herramienta es que, para dos variables aleatorias independientes \(X\) e \(Y\), con sus mgfs que existen alrededor de \(0\), la mgf de \(X+Y\) es el producto de sus respectivas mgfs.

Una función generadora relacionada con la mgf es la función generadora de probabilidad (pgf, según sus siglas en inglés), y es una herramienta útil para las variables aleatorias que toman valores en los números enteros no negativos. Para una variable aleatoria \(N\), por \(P_N(\cdot)\) denotamos su pgf y se define como:³

\[\begin{equation} P_N(s):=\mathrm{E}~{[s^N]}, \quad s\geq 0. \end{equation}\]

Es sencillo ver que si la mgf \(M_N(\cdot)\) existe en \((-\infty,t^\ast)\) entonces \[ P_N(s)=M_N(\log(s)), \quad s<e^{t^\ast}. \] Además, si la pgf existe en el intervalo \([0,s^\ast)\) con \(s^\ast>1\), entonces la mgf \(M_N(\cdot)\) existe en \((-\infty,\log(s^\ast))\), y especifica la distribución de \(N\) de forma única por el Teorema 2.1. El siguiente resultado para pgf es análogo al Teorema 2.1, y en concreto motiva su nombre.

Theorem 2.2 Suponer que \(N\) es una variable aleatoria de tal manera que \(\mathrm{E}~{(s^{\ast})^N}\) es finita para algún \(s^\ast>1\). Se tiene lo siguiente:

Todos los momentos de \(N\) son finitos, i.e. \[ \mathrm{E}~{N^r}<\infty, \quad r\geq 0. \] La pmf de \(N\) se puede derivar de la pgf de la siguiente forma: \[ p_N(m)=\begin{cases} P_N(0), &m=0;\cr &\cr \left(\frac{1}{m!}\right) \left.\frac{{\rm d}^m}{{\rm d}s^m} P_N(s)\right\vert_{s=0}\;, &m\geq 1.\cr \end{cases} \] Los momentos factoriales de \(N\) se pueden derivar de la siguiente manera: \[ \left.\frac{{\rm d}^m}{{\rm d}s^m} P_N(s)\right\vert_{s=1}=\mathrm{E}~{\prod\limits_{i=0}^{m-1} (N-i)}, \quad m\geq 1. \] La pgf \(P_N(\cdot)\) caracteriza la distribución; en otras palabras, especifica de manera única la distribución.

2.2.3 Distribuciones de Frecuencias Importantes

En esta subsección estudiaremos tres importantes distribuciones de frecuencia utilizadas en estadística, que son las distribuciones binomial, Poisson y binomial negativa. En lo siguiente, un riesgo denota una unidad cubierta por el seguro. Un riesgo puede ser un individuo, un edificio, una empresa o algún otro aspecto para el que se proporciona cobertura de seguro. Para contextualizar, imaginemos un conjunto de datos de seguros que contenga el número de siniestros por riesgo o que esté estratificado de alguna otra manera. Las distribuciones mencionadas anteriormente resultan ser también las que más se utilizan en el ámbito asegurador por diferentes razones, algunas de las cuales se mencionan a continuación.

• Estas distribuciones pueden motivarse a partir de experimentos aleatorios que son buenas aproximaciones a los procesos de la vida real de los que surgen muchos datos de seguros. Por lo tanto, no es sorprendente que, en conjunto, ofrezcan un ajuste razonable a muchos conjuntos de datos de interés en seguros. La idoneidad de una distribución concreta para el conjunto de datos puede determinarse utilizando metodologías estadísticas estándar, como se discute más adelante en este capítulo.

• Proporcionan una base suficientemente rica para generar otras distribuciones que se ajustan aún mejor o se adaptan bien a situaciones más reales de interés para nosotros.

  • Las tres distribuciones son de un parámetro o dos parámetros. En el ajuste a los datos al parámetro se le asigna un valor concreto. El conjunto de estas distribuciones puede ampliarse hasta sus envolventes convexas tratando el/los parámetro(s) como una variable aleatoria (o vector) con su propia distribución de probabilidad, con este conjunto más amplio de distribuciones que ofrece una mayor flexibilidad. Un ejemplo sencillo que se aborda mejor con esta ampliación es una cartera de siniestros generada por asegurados pertenecientes a muchas clases de riesgo diferentes.

  • En los datos de seguros se puede observar un número desproporcionado de ceros, es decir, de cero siniestros por riesgo. Al ajustarse a los datos, la distribución de frecuencias en su especificación estándar a menudo no tiene en cuenta suficientemente este hecho. Sin embargo, la modificación natural de las tres distribuciones anteriores se adapta bien a este fenómeno para ofrecer un mejor ajuste.

  • En el seguro nos interesa el total de los siniestros pagados, cuya distribución resulta de la combinación de la distribución de frecuencia ajustada con una distribución de severidad. Estas tres distribuciones tienen propiedades que facilitan trabajar con la distribución de severidad agregada resultante.

2.2.3.1 Distribución Binomial

Empezamos con la distribución binomial que se genera a partir de una secuencia finita de experimentos idénticos e independientes con resultados dicotómicos. El más clásico de estos experimentos es el del lanzamiento de una moneda (trucada o no trucada) con el resultado de cara o cruz. Así, si \(N\) denota el número de caras en una secuencia de \(m\) experimentos independientes del lanzamiento de una moneda idéntica cuya probabilidad de obtener cara es \(q\), entonces la distribución de \(N\) se denomina distribución binomial con parámetros \((m,q)\), con \(m\) un entero positivo y \(q\in[0,1]\). Nótese que cuando \(q=0\) (resp., \(q=1\)) entonces la distribución es degenerada con \(N=0\) (resp., \(N=m\)) con probabilidad \(1\). De forma clara, cuando \(q\in(0,1)\) su suporte es igual a \(\{0,1,\ldots,m\}\) con pmf dada por⁴

\[\begin{equation*} p_k:= \binom{m}{k} q^k (1-q)^{m-k}, \quad k=0,\ldots,m. \end{equation*}\]

donde \[\binom{m}{k} = \frac{m!}{k!(m-k)!}\]

La razón de su nombre es que la pmf toma valores entre los valores que surgen de la expansión binomial \((q +(1-q))^m\). Esta característica nos permite obtener la siguiente expresión para la pgf de la distribución binomial:

\[ P_N(z):= \sum_{k=0}^m z^k \binom{m}{k} q^k (1-q)^{m-k} = \sum_{k=0}^m \binom{m}{k} (zq)^k (1-q)^{m-k} = (qz+(1-q))^m = (1+q(z-1))^m. \]

Nótese que la expresión anterior para la pgf nos confirma que la distribución binomial es la convolución m-ésima de la distribución de Bernoulli, que a su vez es una distribución binomial con \(m=1\) y pgf \((1+q(z-1))\). Además, cabe señalar que la mgf de la distribución binomial viene dada por \((1+q(e^t-1))^m\).

Los momentos centrales de la distribución binomial se pueden encontrar de diferentes maneras. Para enfatizar la propiedad de que se trata de una convulsión \(m\)-ésima de la distribución de Bernoulli, derivamos a continuación los momentos que se basan en esta propiedad. Empezamos observando que la distribución de Bernoulli con parámetro \(q\) asigna la probabilidad de \(q\) y \(1-q\) a \(1\) y \(0\), respectivamente. Así que su media es igual a \(q\) (\(=0\times (1-q) + 1\times q\)); nótese que su segundo momento ordinario es igual a su media como \(N^2=N\) con probabilidad \(1\). Usando estas dos características vemos que la varianza es igual a \(q(1-q)\). Pasando a la distribución binomial con parámetros \(m\) y \(q\), usando el hecho de que es la convolución \(m\)-ésima de la distribución de Bernoulli, escribimos \(N\) como la suma de \(N_1,\ldots,N_m\), donde \(N_i\) son variables de Bernoulli iid. Ahora a partir de los momentos de la Bernoulli y la linealidad de la esperanza, vemos que

\[ \mathrm{E}[{N}]=\mathrm{E}[{\sum_{i=1}^m N_i}] = \sum_{i=1}^m ~\mathrm{E}[N_i] = mq. \] Además, dado que la varianza de la suma de variables aleatorias independientes es la suma de sus varianzas, vemos que

\[ \mathrm{Var}[{N}]=\mathrm{Var}~\left({\sum_{i=1}^m N_i}\right)=\sum_{i=1}^m \mathrm{Var}[{N_i}] = mq(1-q). \]

En los ejercicios se proponen formas alternativas de derivar los momentos anteriores. Es importante remarcar, especialmente desde el punto de vista de las aplicaciones, que la media es mayor que la varianza a menos que \(q=0\).

2.2.3.2 Distribución de Poisson

Después de la distribución binomial, la distribución de Poisson (llamada así por el polímata francés Simeon Denis Poisson) es probablemente la más conocida de las distribuciones discretas. En parte se debe a que surge de forma natural como la distribución de recuento de las ocurrencias aleatorias de un tipo de evento en un determinado período de tiempo, si la tasa de ocurrencia de los eventos es constante. También surge como el límite asintótico de la distribución binomial con \(m\rightarrow \infty\) y \(mq\rightarrow \lambda\).

La distribución de Poisson se parametriza con un único parámetro normalmente denotado por \(\lambda\) que toma valores en \((0,\infty)\). Su pmf viene dada por

\[ p_k = \frac{e^{-\lambda}\lambda^k}{k!}, k=0,1,\ldots \]

Es fácil comprobar que la expresión anterior es una pmf ya que los términos son claramente no-negativos, y a partir de la expansión infinita de la serie de Taylor de \(e^\lambda\) se obtiene que suman uno. De forma genérica, podemos derivar su pgf, \(P(\cdot)\), como sigue:

\[ P_N(z)= \sum_{k=0}^\infty p_k z^k = \sum_{k=0}^\infty \frac{e^{-\lambda}\lambda^kz^k}{k!} = e^{-\lambda} e^{\lambda z} = e^{\lambda(z-1)}, \forall z\in\mathbb{R}. \]

De aquí, derivamos su mgf como sigue:

\[ M_N(t)=P_N(e^t)=e^{\lambda(e^t-1)}, t\in \mathbb{R}. \]

Para obtener su media, observamos que para la distribución de Poisson

\[ kp_k=\begin{cases} 0, &k=0;\cr \lambda~p_{k-1}, &k\geq1. \end{cases} \]

se puede comprobar fácilmente. En particular, lo anterior implica que

\[ \mathrm{E}[{N}]=\sum_{k\geq 0} k~p_k =\lambda\sum_{k\geq 1} p_{k-1} = \lambda\sum_{j\geq 0} p_{j} =\lambda. \] De hecho, de manera más general, utilizando una generalización de lo anterior o el Teorema 2.2, vemos que \[ \mathrm{E}{\prod\limits_{i=0}^{m-1} (N-i)}=\left.\frac{{\rm d}^m}{{\rm d}s^m} P_N(s)\right\vert_{s=1}=\lambda^m, \quad m\geq 1. \] En concreto, lo anterior implica que \[ \mathrm{Var}[{N}]=\mathrm{E}[{N^2}]-[\mathrm{E}({N})]^2 = \mathrm{E}~[N(N-1)]+\mathrm{E}[N]-(\mathrm{E}[{N]})^2=\lambda^2+\lambda-\lambda^2=\lambda. \] Nótese que, curiosamente, para la distribución de Poisson \(\mathrm{Var}[N]=\mathrm{E}[N]\).

2.2.3.3 Distribución Binomial Negativa

La tercera distribución importante de recuento es la distribución binomial negativa. Recordemos que la distribución binomial surge como la distribución del número de éxitos en la repetición independiente de \(m\) veces de un experimento con resultados binarios o dicotómicos. Si por el contrario, consideramos el número de éxitos hasta que observamos el \(r\)-ésimo fallo en repeticiones independientes de un experimento con resultados binarios, entonces su distribución es una distribución binomial negativa. Un caso particular, cuando \(r=1\), es la distribución geométrica. Sin embargo, cuando \(r\) no es un número entero, el experimento aleatorio anterior no sería aplicable. A partir de aquí, permitiremos que el parámetro \(r\) sea cualquier número real positivo, para luego motivar la distribución de manera más general. Para explicar su nombre, recordemos la serie binomial, i.e.

\[ (1+x)^s= 1 + s x + \frac{s(s-1)}{2!}x^2 + \ldots..., \quad s\in\mathbb{R}; \vert x \vert<1. \] Si definimos \(\binom{s}{k}\), el coeficiente binomial generalizado, por \[ \binom{s}{k}=\frac{s(s-1)\cdots(s-k+1)}{k!}, \] tenemos, entonces, que \[ (1+x)^s= \sum_{k=0}^{\infty} \binom{s}{k} x^k, \quad s\in\mathbb{R}; \vert x \vert<1. \] Si fijamos \(s=-r\), entonces observamos que lo anterior genera \[ (1-x)^{-r}= 1 + r x + \frac{(r+1)r}{2!}x^2 + \ldots...= \sum_{k=0}^\infty \binom{r+k-1}{k} x^k, \quad r\in\mathbb{R}; \vert x \vert<1. \] Lo anterior implica que si definimos \(p_k\) como \[ p_k = \binom{k+r-1}{k} \left(\frac{1}{1+\beta}\right)^r \left(\frac{\beta}{1+\beta}\right)^k, \quad k=0,1,\ldots \] para \(r>0\) y \(\beta\geq0\), entonces queda definida una pmf válida. Esta distribución que se ha definido se denomina la distribución negativa binomial con parámetros \((r,\beta)\) con \(r>0\) y \(\beta\geq 0\). Además, la serie binomial también implica que la pgf de la distribución venga dada por \[ \begin{aligned} P_N(z) &= (1-\beta(z-1))^{-r}, \quad \vert z \vert \lt 1+\frac{1}{\beta}, \beta\geq0. \end{aligned} \] Lo anterior implica que la mgf venga dada por \[ \begin{aligned} M_N(t) &= (1-\beta(e^t-1))^{-r}, \quad t \lt \log\left(1+\frac{1}{\beta}\right), \beta\geq0. \end{aligned} \] Derivamos sus momentos utilizando el Teorema 2.1 como sigue:

\[\begin{eqnarray*} \mathrm{E}[N]&=&M'(0)= \left. r\beta e^t (1-\beta(e^t-1))^{-r-1}\right\vert_{t=0}=r\beta;\\ \mathrm{E}[N^2]&=&M''(0)= \left.\left[ r\beta e^t (1-\beta(e^t-1))^{-r-1} + r(r+1)\beta^2 e^{2t} (1-\beta(e^t-1))^{-r-2}\right]\right\vert_{t=0}\\ &=&r\beta(1+\beta)+r^2\beta^2;\\ \hbox{y }\mathrm{Var}[N]&=&\mathrm{E}{[N^2]}-(\mathrm{E}[{N}])^2=r\beta(1+\beta)+r^2\beta^2-r^2\beta^2=r\beta(1+\beta) \end{eqnarray*}\]

Observamos que cuando \(\beta>0\), tenemos \(\mathrm{Var}[N] >\mathrm{E}[N]\). En otras palabras, esta distribución es sobredispersa (en relación a la Poisson); de manera similar, cuando \(q>0\) la distribución binomial se dice que es infradispersa (en relación a la Poisson).

Finalmente, observamos que la distribución de Poisson también surge como límite de distribuciones binomiales negativas. Para establecer esto, fijamos \(\beta_r\) de tal forma que cuando \(r\) tienda a infinito \(r\beta_r\) tiende a \(\lambda>0\). Entonces, podemos ver que las mgfs de las distribuciones binomiales negativas con parámetros \((r,\beta_r)\) satisfacen

\[ \lim_{r\rightarrow 0} (1-\beta_r(e^t-1))^{-r}=\exp\{\lambda(e^t-1)\}, \] con el lado derecho de la ecuación anterior siendo la mgf de la distribución de Poisson con parámetro \(\lambda\).⁵

2.3 La Clase (a, b, 0)

---

En esta sección, se aprende a:

• Definir la clase (a,b,0) de distribuciones de frecuencia
• Discutir la importancia de la relación recursiva que sustenta esta clase de distribuciones
• Identificar las condiciones en las que esta clase general se reduce a cada una de las distribuciones binomial, Poisson y binomial negativa

---

En la sección anterior estudiamos tres distribuciones, en concreto, la binomial, la Poisson y la binomial negativa. En el caso de la Poisson, para obtener su media usamos el hecho que

\[ kp_k=\lambda p_{k-1}, \quad k\geq 1, \] lo que se puede expresar de forma equivalente como \[ \frac{p_k}{p_{k-1}}=\frac{\lambda}{k}, \quad k\geq 1. \]

Curiosamente, se puede mostrar de forma similar que para la distribución binomial

\[ \frac{p_k}{p_{k-1}}=\frac{-q}{1-q}+\left(\frac{(m+1)q}{1-q}\right)\frac{1}{k}, \quad k=1,\ldots,m, \] y para la distribución binomial negativa \[ \frac{p_k}{p_{k-1}}=\frac{\beta}{1+\beta}+\left(\frac{(r-1)\beta}{1+\beta}\right)\frac{1}{k}, \quad k\geq 1. \] Las tres relaciones previas son de la forma \[\begin{equation} \frac{p_k}{p_{k-1}}=a+\frac{b}{k}, \quad k\geq 1; \tag{2.1} \end{equation}\]

esto plantea la cuestión de si hay otras distribuciones que satisfagan esta relación de recurrencia aparentemente general. Nótese que la relación de la izquierda, el cociente entre dos probabilidades, es no negativa.

Para empezar, permitamos \(a<0\). En este caso, como \(k\rightarrow \infty\), \((a+b/k)\rightarrow a<0\). De esto se deduce que si \(a<0\) entonces \(b\) debería satisfacer \(b=-ka\), para \(k\geq 1\). Cualquier par \((a,b)\) puede escribirse como

\[ \left(\frac{-q}{1-q},\frac{(m+1)q}{1-q}\right), \quad q\in(0,1), m\geq 1; \] nótese que en el caso \(a<0\) con \(a+b=0\) produce la degenerada de una distribución de \(0\) que es la distribución binomial con \(q=0\) y un arbitrario \(m\geq 1\).

En el caso de \(a=0\), de nuevo por la no negatividad de la proporción \(p_k/p_{k-1}\), tenemos \(b\geq 0\). Si \(b=0\) la distribución es degenerada en \(0\), que es una binomial con \(q=0\) o una distribución de Poisson con \(\lambda=0\) o una distribución binomial negativa con \(\beta=0\). Si \(b>0\), entonces de forma clara esta distribución es una distribución de Poisson con una media (i.e. \(\lambda\)) igual a \(b\), como se muestra al principio de esta sección.

En el caso de \(a>0\), de nuevo por la no negatividad de la proporción \(p_k/p_{k-1}\), tenemos \(a+b/k\geq 0\) para todo \(k\geq 1\). La más estricta de estas es la desigualdad \(a+b\geq 0\). Nótese que \(a+b=0\) de nuevo resulta en una degenerada en \(0\); excluyendo este caso tenemos \(a+b>0\) o equivalentemente \(b=(r-1)a\) con \(r>0\). Después de un poco de álgebra, fácilmente se obtiene la siguiente expresión para \(p_k\):

\[ p_k = \binom{k+r-1}{k} p_0 a^k, \quad k=1,2,\ldots. \] La serie anterior converge a \(a<1\) cuando \(r>0\), con la suma dada por \(p_0*((1-a)^{(-r)}-1)\). Por lo tanto, al igualar este último a \(1-p_0\) obtenemos \(p_0=(1-a)^{(r)}\). Así, en este caso el par \((a,b)\) es de la forma \((a,(r-1)a)\), para \(r>0\) y \(0<a<1\); ya que una parametrización equivalente es \((\beta/(1+\beta),(r-1)\beta/(1+\beta))\), para \(r>0\) y \(\beta>0\), vemos de lo anterior que estas distribuciones son distribuciones binomiales negativas.

A partir del desarrollo anterior vemos que no sólo la recurrencia (2.1) une estas tres distribuciones, sino que también las caracteriza. Por esta razón, estas tres distribuciones se denominan de forma genérica en la literatura actuarial como clase (a,b,0) de distribuciones, con \(0\) haciendo referencia al punto inicial de la recurrencia. Nótese que el valor de \(p_0\) está implícito en \((a,b)\) ya que las probabilidades tienen que sumar uno. Por supuesto, (2.1) como relación de recurrencia para \(p_k\), hace que el cálculo de la pmf sea eficiente al eliminar las redundancias. Más adelante veremos que lo hace incluso en el caso de distribuciones compuestas con la distribución de frecuencias perteneciente a la clase \((a,b,0)\) - esta característica es la razón más importante para justificar el estudio de estas tres distribuciones desde este punto de vista.

Ejemplo 2.3.1. Una distribución de probabilidad discreta tiene las siguientes propiedades \[ \begin{aligned} p_k&=c\left( 1+\frac{2}{k}\right) p_{k-1} \:\:\: k=1,2,3,\ldots\\ p_1&= \frac{9}{256} \end{aligned} \] Determinar el valor esperado de esta variable aleatoria discreta.

Mostrar Solución de Ejemplo

Solución: Dado que la pmf satisface la relación de recurrencia \((a,b,0)\) sabemos que la distribución subyacente es una entre las distribuciones binomial, Poisson y binomial negativa. Puesto que la relación de los parámetros (i.e. \(b/a\)) es igual a \(2\), sabemos que es binomial negativa y que \(r=3\). Además, ya que para la binomial negativa \(p_1=r(1+\beta)^{-(r+1)}\beta\), tenemos

\[ \begin{aligned} &&\frac{9}{256}=&3\frac{\beta}{(1+\beta)^4}\\ \implies &&\frac{3}{(1+3)^4}=&\frac{\beta}{(1+\beta)^4}\\ \implies &&\beta=&3. \end{aligned} \] Por último, dado que la media de la binomial negativa es \(r\beta\), tenemos que la media de esta distribución es igual a \(9\).

---

2.4 Estimación de las Distribuciones de Frecuencias

---

En esta sección, se aprende a:

• Definir la verosimilitud para una muestra de observaciones de una distribución discreta
• Definir el estimador de máxima verosimilitud para una muestra aleatoria de observaciones de una distribución discreta
• Calcular el estimador de máxima verosimilitud para las distribuciones binomial, Poisson y binomial negativa

---

2.4.1 Estimación de los parámetros

En la sección 2.2 se introdujeron tres distribuciones muy importantes para la modelización de varios tipos de datos de recuento derivados de los seguros. Supongamos ahora que tenemos un conjunto de datos de recuento a los que queremos ajustar una distribución, y hemos determinado que una de las distribuciones \((a,b,0)\) es más apropiada que las otras. Dado que cada una de ellas forma una clase de distribuciones si permitimos que su(s) parámetro(s) tome(n) cualquier valor permisible, queda la tarea de determinar el mejor valor del(los) parámetro(s) para los datos en cuestión. Éste es un problema estadístico de estimación puntual, y el paradigma de inferencia estadística de máxima verosimilitud suele producir estimadores eficientes en los problemas de inferencia paramétrica. En esta sección describiremos este paradigma y derivaremos los estimadores de máxima verosimilitud.

Supongamos que observamos las variables aleatorias independientes e idénticamente distribuidas, iid, \(X_1,X_2,\ldots,X_n\) de una distribución con pmf \(p_\theta\), donde \(\theta\) es un parámetro y un valor desconocido en el espacio del parámetro \(\Theta\subseteq \mathbb{R}^d\). Por ejemplo, en el caso de la distribución de Poisson

\[ p_\theta(x)=e^{-\theta}\frac{\theta^x}{x!}, \quad x=0,1,\ldots, \] con \(\theta=(0,\infty)\). En el caso de la distribución binomial, tenemos \[ p_\theta(x)=\binom{m}{x} q^x(1-q)^{m-x}, \quad x=0,1,\ldots,m, \] con \(\theta:=(m,q)\in \{0,1,2,\ldots\}\times[0,1]\). Supongamos que las observaciones son \(x_1,\ldots,x_n\), valores observados de la muestra aleatoria \(X_1,X_2,\ldots,X_n\) presentada anteriormente. En este caso, la probabilidad de observar esta muestra a partir de \(p_\theta\) es igual a

\[ \prod_{i=1}^n p_\theta(x_i). \] Lo anterior, denotado por \(L(\theta)\), visto como una función de \(\theta\) se denomina la verosimilitud. Nótese que eliminamos su dependencia de los datos, para enfatizar que lo estamos viendo como una función del parámetro. Por ejemplo, en el caso de la distribución de Poisson tenemos

\[ L(\lambda)=e^{-n\lambda} \lambda^{\sum_{i=1}^n x_i} \left(\prod_{i=1}^n x_i!\right)^{-1}; \] en el caso de la distribución binomial tenemos \[ L(m,q)=\left(\prod_{i=1}^n \binom{m}{x_i}\right) q^{\sum_{i=1}^n x_i} (1-q)^{nm-\sum_{i=1}^n x_i} . \] El estimador máximo verosímil (MLE, según sus siglas en inglés) para \(\theta\) es un maximizador de la verosimilitud; en cierto sentido, el MLE elige el conjunto de valores de los parámetros que mejor explican las observaciones observadas. Consideremos una muestra de tamaño \(3\) de una distribución de Bernoulli (binomial con \(m=1\)) con valores de \(0,1,0\). En este caso se comprueba fácilmente que la verosimilitud es igual a

\[ L(q)=q(1-q)^2, \] y el gráfico de la verosimilitud se muestra en la Figura 2.1. Como se muestra en el gráfico, el valor máximo de la verosimilitud es igual a \(4/27\) y se alcanza en \(q=1/3\), y por lo tanto el estimador máximo verosímil para \(q\) es \(1/3\) para la muestra considerada. En este caso se puede recurrir al álgebra para mostrar que \[ q(1-q)^2=\left(q-\frac{1}{3}\right)^2\left(q-\frac{4}{3}\right)+\frac{4}{27}, \]

y concluir que el máximo es igual a \(4/27\), y se alcanza en \(q=1/3\) (usando el hecho de que el primer término es no positivo en el intervalo \([0,1]\)). Pero como es evidente, esta forma de derivar el mle utilizando el álgebra no es generalizada. Normalmente, se recurre al cálculo para derivar el mle - obsérvese que para algunas verosimilitudes uno puede tener que recurrir a otros métodos de optimización, especialmente cuando la verosimilitud tiene muchos extremos locales. Se acostumbra a maximizar de forma equivalente el logaritmo de la verosimilitud⁶ \(L(\cdot)\), denotado por \(l(\cdot)\), y mirar el conjunto de ceros de su primera derivada⁷ \(l'(\cdot)\). En el caso de la verosimilitud anterior, \(l(q)=\log(q)+2\log(1-q)\), y

\[ l'(q):=\frac{\rm d}{{\rm d}q}l(q)=\frac{1}{q}-\frac{2}{1-q}. \] El único cero de \(l'(\cdot)\) iguala a \(1/3\), y dado que \(l''(\cdot)\) es negativa, tenemos que \(1/3\) es el único maximizador de la verosimilitud y por tanto su estimador máximo verosímil.

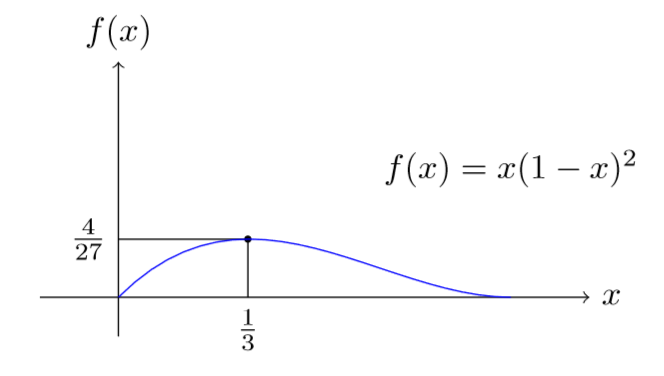
Figure 2.1: Verosimilitud para \((0,1,0)\) de una muestra de \(3\) de una Bernoulli

2.4.2 MLE de las distribuciones de frecuencias

A continuación derivamos el estimador de máxima verosimilitud, MLE, para los tres miembros de la clase \((a,b,0)\). Empezamos resumiendo la discusión anterior. En el escenario de observar las variables aleatorias iid, independientes e idénticamente distribuidas, \(X_1,X_2,\ldots,X_n\) de una distribución con pmf \(p_\theta\), donde \(\theta\) toma un valor desconocido en \(\Theta\subseteq \mathbb{R}^d\), la verosimilitud \(L(\cdot)\), una función en \(\Theta\) se define como

\[ L(\theta):=\prod_{i=1}^n p_\theta(x_i), \] donde \(x_1,\ldots,x_n\) son los valores observados. El MLE de \(\theta\), denotado como \(\hat{\theta}_{\rm MLE}\), es una función que asigna las observaciones a un elemento del conjunto de maximizadores de \(L(\cdot)\), concretamente \[ \{\theta \vert L(\theta)=\max_{\eta\in\Theta}L(\eta)\}. \] Nótese que el conjunto anterior es una función de las observaciones, aunque esta dependencia no se muestra explícitamente. En el caso de las tres distribuciones que estudiaremos, y de forma bastante general, el conjunto anterior es un conjunto unitario (singleton) con una probabilidad que tiende a uno (con un tamaño de muestra creciente). En otras palabras, para muchas distribuciones de uso común y cuando el tamaño de la muestra es grande, el estimador verosímil se define de forma única con una alta probabilidad. A continuación, asumiremos que hemos observado \(n\) variables aleatorias iid \(X_1,X_2,\ldots,X_n\) de la distribución considerada, aunque el valor del parámetro es desconocido. Además, \(x_1,x_2,\ldots,x_n\) denotará los valores observados. Cabe señalar en el caso de los datos de recuento, y de los datos de distribuciones discretas en general, que la verosimilitud puede representarse alternativamente como

\[ L(\theta):=\prod_{k\geq 0} \left(p_\theta(k)\right)^{m_k}, \] donde \[ m_k:= \left\vert \{i\vert x_i=k, 1\leq i \leq n\} \right\vert=\sum_{i= 1}^n I(x_i=k), \quad k\geq 0. \] Obsérvese que esta transformación conserva todos los datos, compilándolos de manera racionalizada. Para un \(n\) grande, lleva a la compresión de los datos en el sentido de suficiencia. A continuación, presentamos las expresiones para el MLE también en términos de \(\{m_k\}_{k\geq 1}\).

MLE – Distribución de Poisson: En este caso, como se ha señalado anteriormente, la verosimilitud viene dada por \[ L(\lambda)=\left(\prod_{i=1}^n x_i!\right)^{-1}e^{-n\lambda}\lambda^{\sum_{i=1}^n x_i}, \] que implica \[ l(\lambda)= -\sum_{i=1}^n \log(x_i!) -n\lambda +\log(\lambda) \cdot \sum_{i=1}^n x_i, \] y \[ l'(\lambda)= -n +\frac{1}{\lambda}\sum_{i=1}^n x_i. \]

En la evaluación de \(l''(\lambda)\), cuando \(\sum_{i=1}^n x_i>0\), \(l''< 0\). Por consiguiente, el máximo se alcanza en la media de la muestra, \(\overline{x}\), que se presenta a continuación. Cuando \(\sum_{i=1}^n x_i=0\), la verosimilitud es una función decreciente y, por lo tanto, el máximo se alcanza en el menor valor posible del parámetro; esto da como resultado que el estimador máximo verosímil sea cero. Por lo tanto, tenemos

\[ \overline{x} = \hat{\lambda}_{\rm MLE} = \frac{1}{n}\sum_{i=1}^n x_i. \] Nótese que la media muestral puede calcularse también como \[ \frac{1}{n} \sum_{k\geq 1} km_k. \]

Cabe mencionar que en el caso de la Poisson, la distribución exacta de \(\hat{\lambda}_{\rm MLE}\) está disponible en forma cerrada - es una Poisson a escala - cuando la distribución subyacente es una Poisson. Esto es así porque la suma de variables aleatorias independientes de Poisson es también una Poisson. Por supuesto, para muestras de gran tamaño se puede utilizar el Teorema Central del Límite (CLT, según sus siglas en inglés) ordinario para derivar una aproximación normal. Nótese que esta última aproximación es válida si la distribución subyacente es una distribución con un segundo momento finito.

MLE – Distribución Binomial: A diferencia del caso de la distribución de Poisson, el espacio de parámetros en el caso de la binomial es bidimensional. Por lo tanto, el problema de optimización es un poco más difícil. Podemos comenzar observando que la verosimilitud viene dada por

\[ L(m,q)= \left(\prod_{i=1}^n \binom{m}{x_i}\right) q^{\sum_{i=1}^n x_i} (1-q)^{nm-\sum_{i=1}^n x_i}, \] y el logaritmo de la verosimilitud por \[ l(m,q)= \sum_{i=1}^n \log\left(\binom{m}{x_i}\right) + \left({\sum_{i=1}^n x_i}\right)\log(q)+ \left({nm-\sum_{i=1}^n x_i}\right)\log(1-q). \] Nótese que como \(m\) sólo toma valores enteros no negativos, no podemos usar cálculo multivariante para encontrar los valores óptimos. Sin embargo, podemos usar el cálculo para una sola variable para mostrar que \[\begin{equation} \hat{q}_{\rm MLE}\times \hat{m}_{\rm MLE}= \frac{1}{n}\sum_{i=1}^n X_i. \tag{2.2} \end{equation}\] En este sentido, observamos que para un valor fijado de \(m\), \[ \frac{\delta}{\delta q} l(m,q) = \left({\sum_{i=1}^n x_i}\right)\frac{1}{q}- \left({nm-\sum_{i=1}^n x_i}\right)\frac{1}{1-q}, \] y que \[ \frac{\delta^2}{\delta q^2} l(m,q) = -\left[\left({\sum_{i=1}^n x_i}\right)\frac{1}{q^2} + \left({nm-\sum_{i=1}^n x_i}\right)\frac{1}{(1-q)^2}\right]\leq 0. \] Lo anterior implica que para un valor concreto de \(m\), el valor máximo de \(q\) satisface \[ mq=\frac{1}{n}\sum_{i=1}^n X_i, \] y por lo tanto establecemos la ecuación (2.2). Lo anterior reduce la tarea a la búsqueda de \(\hat{m}_{\rm MLE}\), que es miembro del conjunto de los maximizadores de \[\begin{equation} L\left(m,\frac{1}{nm}\sum_{i=1}^n x_i\right). \tag{2.3} \end{equation}\] Nótese que la verosimilitud sería cero para valores de \(m\) menores a \(\max\limits_{1\leq i \leq n}x_i\), y por tanto \[ \hat{m}_{\rm MLE}\geq \max_{1\leq i \leq n}x_i. \] Para especificar un algoritmo para calcular \(\hat{m}_{\rm MLE}\), primero señalamos que para algunos conjuntos de datos \(\hat{m}_{\rm MLE}\) podría ser igual a \(\infty\), lo que indicaría que una distribución de Poisson se ajustaría mejor que una distribución binomial. Esto es así, ya que la distribución binomial con los parámetros \((m,\overline{x}/m)\) se aproxima a la distribución de Poisson con el parámetro \(\overline{x}\) con \(m\) tendiendo a infinito. El hecho de que algunos conjuntos de datos prefieran una distribución de Poisson no debería ser sorprendente ya que desde este punto de vista el conjunto de la distribución de Poisson está en el límite del conjunto de las distribuciones binomiales.

Curiosamente, en (Olkin, Petkau, and Zidek 1981) muestran que si la media de la muestra es menor o igual a la varianza de la muestra entonces \(\hat{m}_{\rm MLE}=\infty\); de lo contrario, existe un \(m\) finito que maximiza la ecuación (2.3). En la siguiente Figura 2.2 se muestra el gráfico de \(L\left(m,\frac{1}{nm}\sum_{i=1}^n x_i\right)\) para tres muestras diferentes de tamaño \(5\); sólo difieren en el valor del máximo de la muestra. La primera muestra de \((2,2,2,4,5)\) tiene una relación entre la media de la muestra y la varianza de la muestra mayor a \(1\) (\(1,875\)), la segunda muestra de \((2,2,2,4,6)\) tiene la relación igual a \(1,25\) que está más cerca de \(1\), y la tercera muestra de \((2,2,2,4,7)\) tiene una relación menor a \(1\) (\(0,885\)). Para las tres muestras, como se muestra en la Figura 2.2, \(\hat{m}_{\rm MLE}\) es igual a \(7\), \(18\) and \(\infty\), respectivamente. Nótese que el valor en el límite de \(L\left(m,\frac{1}{nm}\sum_{i=1}^n x_i\right)\) cuando \(m\) tiende a infinito es igual a

\[\begin{equation} \left(\prod_{i=1}^n x_i! \right)^{-1} \exp\left\{-\sum_{i=1}^n x_i\right\} \overline{x}^{n\overline{x}}. \tag{2.4} \end{equation}\] También, se debe señalar que la Figura 2.2 muestra que el MLE de \(m\) es no robusto, i.e., pequeños cambios en el conjunto de datos pueden causar grandes cambios en el estimador.

La discusión anterior sugiere el siguiente algoritmo sencillo:

• Paso 1. Si la media de la muestra es menor o igual a la varianza de la muestra, \(\hat{m}_{MLE}=\infty\). La distribución sugerida por MLE es una distribución de Poisson con \(\hat{\lambda}=\overline{x}\).

• Paso 2. Si la media de la muestra es mayor que la varianza de la muestra, entonces calcula \(L(m,\overline{x}/m)\) para valores de \(m\) mayores o iguales al máximo de la muestra hasta que \(L(m,\overline{x}/m)\) se acerque al valor de la verosimilitud de Poisson dada en (2.4). El valor de \(m\) que corresponde al valor máximo de \(L(m,\overline{x}/m)\) entre los calculados es igual a \(\hat{m}_{MLE}\).

Obsérvese que si la distribución subyacente es la distribución binomial con parámetros \((m,q)\) (con \(q>0\)) entonces \(\hat{m}_{MLE}\) será igual a \(m\) para los tamaños de muestra grandes. Además, \(\hat{q}_{MLE}\) tendrá una distribución asintóticamente normal y convergerá con probabilidad uno a \(q\).

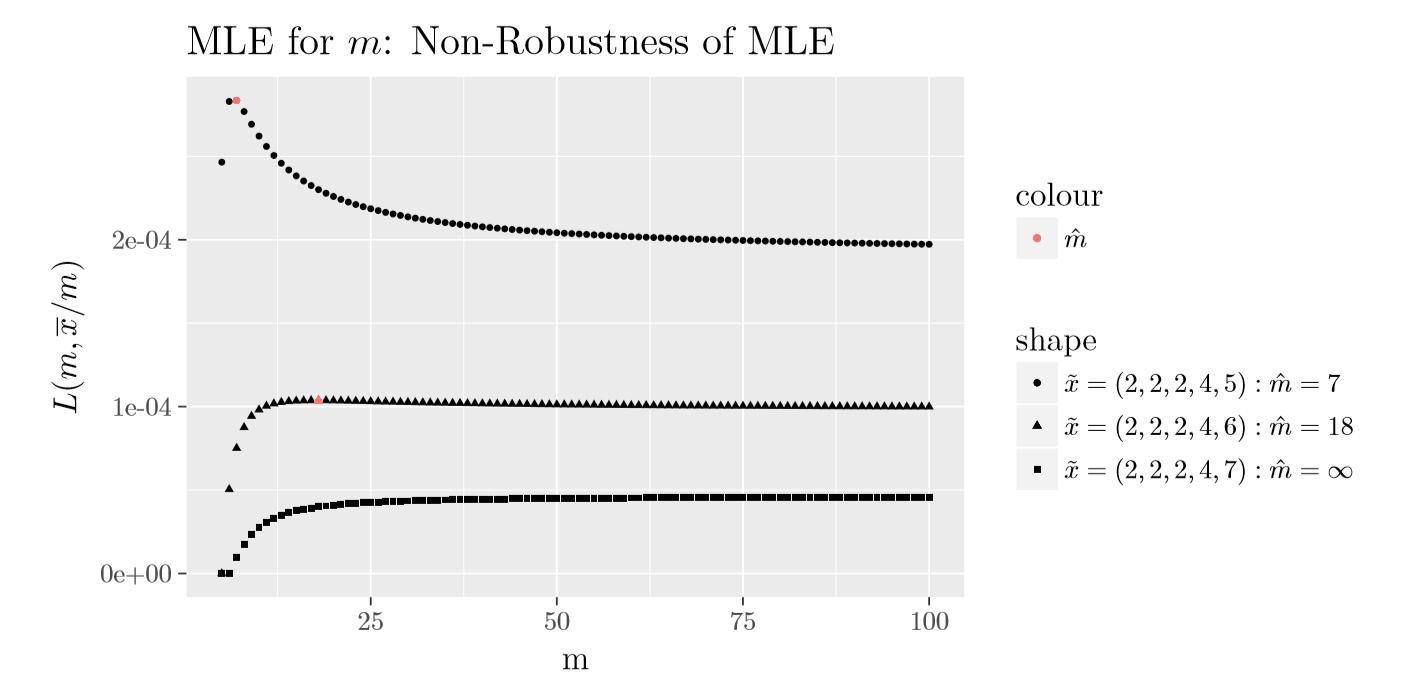
Figure 2.2: Gráfico de \(L(m,\overline{x}/m)\) de la distribución binomial

MLE – Distribución Binomial Negativa: El caso de la distribución binomial negativa es similar al de la distribución binomial en el sentido de que tenemos dos parámetros y los MLE no existen en una forma cerrada. Una diferencia entre ellas es que, a diferencia del parámetro de la binomial \(m\) que toma valores enteros positivos, el parámetro \(r\) de la binomial negativa puede tomar cualquier valor real positivo. Esto hace que el problema de optimización sea un poco más complejo. Comencemos señalando que la verosimilitud puede expresarse de la siguiente forma:

\[ L(r,\beta)=\left(\prod_{i=1}^n \binom{r+x_i-1}{x_i}\right) (1+\beta)^{-n(r+\overline{x})} \beta^{n\overline{x}}. \] Lo anterior implica que la log-verosimilitud viene dada por \[ l(r,\beta)=\sum_{i=1}^n \log\binom{r+x_i-1}{x_i} -n(r+\overline{x}) \log(1+\beta) +n\overline{x}\log\beta, \] Y por tanto \[ \frac{\delta}{\delta\beta} l(r,\beta) = -\frac{n(r+\overline{x})}{1+\beta} + \frac{n\overline{x}}{\beta}. \] Igualando la ecuación a cero, tenemos \[ \hat{r}_{MLE}\times \hat{\beta}_{MLE} = \overline{x}. \] Lo anterior reduce el problema de optimización bidimensional a un problema unidimensional- se necesita maximizar \[ l(r,\overline{x}/r)=\sum_{i=1}^n \log\binom{r+x_i-1}{x_i} -n(r+\overline{x}) \log(1+\overline{x}/r) +n\overline{x}\log(\overline{x}/r), \] con respecto a \(r\), siendo el maximizador de \(r\) su MLE y \(\hat{\beta}_{MLE}=\overline{x}/\hat{r}_{MLE}\). En (Levin, Reeds, and others 1977) se muestra que si la varianza muestral es mayor que la media muestral, entonces existe un único \(r>0\) que maximiza \(l(r,\overline{x}/r)\) y por lo tanto un único MLE para \(r\) y \(\beta\). Además, muestran que si \(\hat{\sigma}^2\leq \overline{x}\), entonces la verosimilitud de la binomial negativa estará dominada por la verosimilitud de la Poisson con \(\hat{\lambda}=\overline{x}\). En otras palabras, una distribución de Poisson ofrece un mejor ajuste a los datos. La garantía en el caso de \(\hat{\sigma}^2>\hat{\mu}\) nos permite usar un algoritmo para maximizar \(l(r,\overline{x}/r)\). Mediante un método alternativo de calcular la verosimilitud, observamos que \[ l(r,\overline{x}/r)=\sum_{i=1}^n \sum_{j=1}^{x_i}\log(r-1+j) - \sum_{i=1}^n\log(x_i!) - n(r+\overline{x}) \log(r+\overline{x}) + nr\log(r) + n\overline{x}\log(\overline{x}), \] lo que genera \[ \left(\frac{1}{n}\right)\frac{\delta}{\delta r}l(r,\overline{x}/r)=\left(\frac{1}{n}\right)\sum_{i=1}^n \sum_{j=1}^{x_i}\frac{1}{r-1+j} - \log(r+\overline{x}) + \log(r). \] Observamos que, en las expresiones anteriores para los términos que implican un doble sumatorio, el sumatorio interno es igual a cero si \(x_i=0\). El estimador máximo verosímil de \(r\) es una raíz de la última expresión y podemos usar un algoritmo de búsqueda de raíces para calcularla. Además, tenemos

\[ \left(\frac{1}{n}\right)\frac{\delta^2}{\delta r^2}l(r,\overline{x}/r)=\frac{\overline{x}}{r(r+\overline{x})}-\left(\frac{1}{n}\right)\sum_{i=1}^n \sum_{j=1}^{x_i}\frac{1}{(r-1+j)^2}. \] Un algoritmo iterativo de búsqueda de raíces simple y de rápida convergencia es el método de Newton, que se cree que los Babilonios ya utilizaban para calcular raíces cuadradas. Con este método, se selecciona una aproximación inicial para la raíz y se generan sucesivamente nuevas aproximaciones para la raíz hasta la convergencia. Aplicando el método de Newton a nuestro problema se obtiene el siguiente algoritmo:
Paso i. Elegir una solución aproximada, denominada \(r_0\). Fijar \(k\) igual a \(0\).
Paso ii. Definir \(r_{k+1}\) como \[ r_{k+1}:= r_k - \frac{\left(\frac{1}{n}\right)\sum_{i=1}^n \sum_{j=1}^{x_i}\frac{1}{r_k-1+j} - \log(r_k+\overline{x}) + \log(r_k)}{\frac{\overline{x}}{r_k(r_k+\overline{x})}-\left(\frac{1}{n}\right)\sum_{i=1}^n \sum_{j=1}^{x_i}\frac{1}{(r_k-1+j)^2}} \]
Paso iii. Si \(r_{k+1}\sim r_k\), entonces establece \(r_{k+1}\) como estimador máximo verosímil; en otro caso, incrementa \(k\) por \(1\) y repite Paso ii.

Por ejemplo, simulamos una muestra de \(5\) observaciones de \(41, 49, 40, 27, 23\) de la binomial negativa con los parámetros \(r=10\) y \(\beta=5\). Escogiendo el valor inicial de \(r\) de tal manera que \[ r\beta=\hat{\mu} \quad \hbox{and} \quad r\beta(1+\beta)=\hat{\sigma}^2 \] donde \(\hat{\mu}\) representa la media estimada y \(\hat{\sigma}^2\) es la varianza estimada. Esto nos conduce a un valor inicial de \(r\) de \(23,14286\). Las iteraciones de \(r\) del método de Newton son \[ 21,39627, 21,60287, 21,60647, 21,60647; \] la rápida convergencia anterior es frecuente con el método de Newton. Por lo tanto, en este ejemplo, \(\hat{r}_{MLE}\sim21,60647\) y \(\hat{\beta}_{MLE}=8,3308\).

Implementación R del Método de Newton - MLE binomial negativa para \(r\)

Mostrar Código R

Newton<-function(x,abserr){
mu<-mean(x);
sigma2<-mean(x^2)-mu^2;
r<-mu^2/(sigma2-mu);
b<-TRUE;
iter<-0;
while (b) {
tr<-r;
m1<-mean(c(x[x==0],sapply(x[x>0],function(z){sum(1/(tr:(tr-1+z)))})));
m2<-mean(c(x[x==0],sapply(x[x>0],function(z){sum(1/(tr:(tr-1+z))^2)})));
r<-tr-(m1-log(1+mu/tr))/(mu/(tr*(tr+mu))-m2);
b<-!(abs(tr-r)<abserr);
iter<-iter+1;
}
c(r,iter)
}

---

Para concluir nuestra discusión sobre MLE para la clase de distribuciones \((a,b,0)\), en la Figura 2.3 siguiente representamos gráficamente el valor máximo de la verosimilitud de Poisson, \(L(m,\overline{x}/m)\) para la binomial, y \(L(r,\overline{x}/r)\) para la binomial negativa, para las tres muestras de tamaño \(5\) dadas en Tabla 2.1. Los datos se construyeron de tal forma que cubrieran las tres ordenaciones entre la media y varianza muestrales. Como se muestra en la Figura 2.3, y demostrado por la teoría, si \(\hat{\mu}<\hat{\sigma}^2\) entonces la binomial negativa dará un mayor valor del máximo de verosimilitud; si \(\hat{\mu}=\hat{\sigma}^2\) la Poisson dará el mayor valor de la verosimilitud; y finalmente en el caso que \(\hat{\mu}>\hat{\sigma}^2\) la binomial dará un mejor ajuste que las otras. Así que, antes de ajustar los datos con una distribución de frecuencias \((a,b,0)\), es mejor empezar por examinar el orden entre \(\hat{\mu}\) y \(\hat{\sigma}^2\). Cabe volver a enfatizar que la Poisson está en el límite de las distribuciones binomial negativa y binomial. Por lo tanto en el caso que \(\hat{\mu}\geq\hat{\sigma}^2\) (\(\hat{\mu}\leq\hat{\sigma}^2\), resp.) la Poisson dará un mejor ajuste que la binomial negativa (binomial, resp.), que también se indicará con \(\hat{r}=\infty\) (\(\hat{m}=\infty\), resp.).

\[\begin{matrix} \begin{array}{c|c|c} \hline \text{Datos} & \text{Media }(\hat{\mu}) & \text{Varianza }(\hat{\sigma}^2) \\ \hline (2,3,6,8,9) & 5,60 & 7,44 \\ (2,5,6,8,9) & 6 & 6\\ (4,7,8,10,11) & 8 & 6\\\hline \end{array} \end{matrix}\]

Tabla 2.1 : Tres Muestras de Tamaño \(5\)

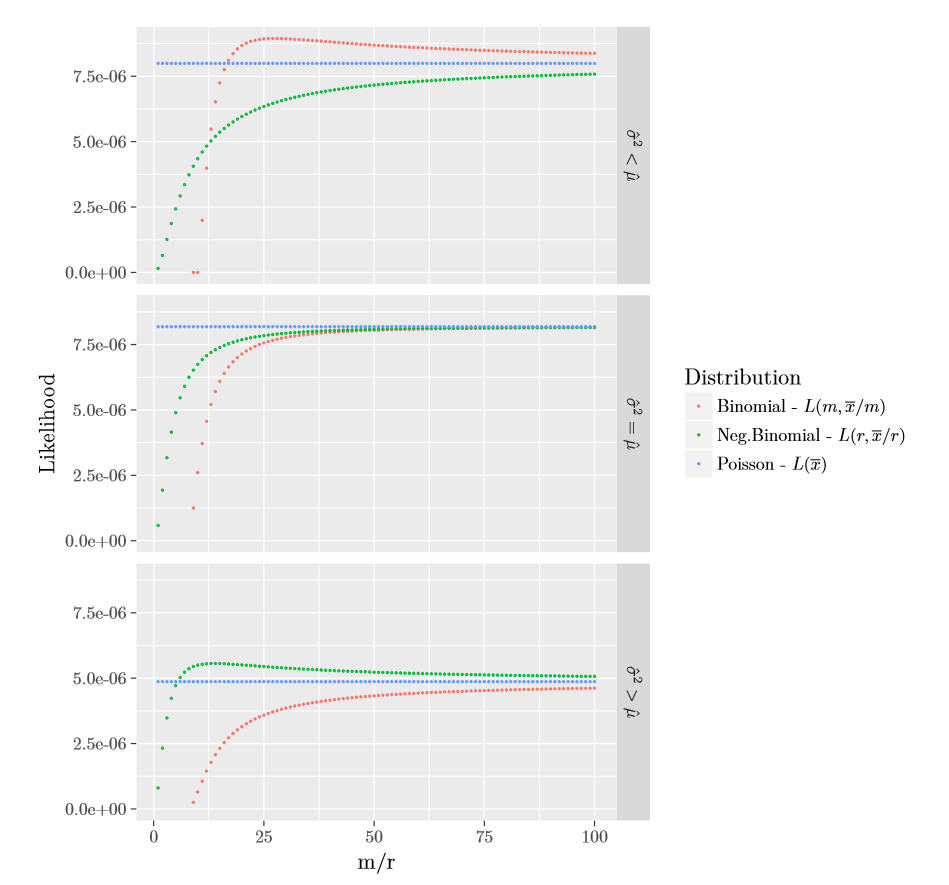
Figure 2.3: Gráfico de las Verosimilitudes Parcialmente Maximizadas \((a,b,0)\)

2.5 Otras Distribuciones de Frecuencias

---

En esta sección, se aprende a:

• Definir la clase de distribuciones de frecuencia (a,b,1) y discutir la importancia de la relación recursiva que sustenta esta clase de distribuciones
• Interpretar las versiones truncadas y modificadas en cero de las distribuciones binomiales, Poisson y binomial negativa
• Calcular las probabilidades usando la relación recursiva

---

En las secciones anteriores hemos examinado tres distribuciones con soporte definido en el conjunto de números enteros no negativos, que se adaptan bien a muchas aplicaciones de seguros. Además, al permitir frecuentemente que los parámetros sean una función de variables explicativas conocidas (por el asegurador) como la edad, el sexo, la ubicación geográfica (territorio), etc., estas distribuciones nos permiten explicar las probabilidades de siniestro en términos de estas variables. El ámbito de la estadística que analiza estos modelos se conoce como análisis de regresión - es un tópico importante de interés actuarial que no se tratará en este libro; ver (Edward W Frees 2009).

Es evidente que existen infinitas otras distribuciones de recuento, y lo que es más importante, las distribuciones anteriores por sí mismas no satisfacen todas las necesidades prácticas. En concreto, una característica de algunos datos en seguros es que la proporción de ceros puede ser muy diferente en la relación a la proporción de otros valores para que puedan ser explicados por las distribuciones anteriores. A continuación, se modifican las distribuciones previas para permitir una probabilidad arbitraria para el recuento de ceros, independientemente de la asignación relativa de probabilidades para los otros valores. Otra característica de un conjunto de datos que está compuesto por subconjuntos homogéneos es que, aunque las distribuciones anteriores pueden proporcionar buenos ajustes a cada subconjunto, pueden no hacerlo para la totalidad del conjunto de datos. Posteriormente, se amplían de forma natural las distribuciones \((a,b,0)\) para poder cubrir, en particular, estos conjuntos de datos.

2.5.1 Modificación o Truncamiento en Cero

Supongamos que analizamos pólizas del seguro de automóvil que aparecen en una base de datos de siniestros de automóvil ocurridos en un determinado período. Si se estudia el número de siniestros que estas pólizas han tenido durante este período, entonces obviamente la distribución tiene que asignar una probabilidad de cero a la variable de recuento que asume el valor cero. En otras palabras, al restringir la atención a los datos de recuento en las pólizas de la base de datos de siniestros, en cierto modo hemos truncado en cero los datos de recuento de todas las pólizas. En productos de seguros a particulares (como en el caso de los automóviles), los asegurados pueden no querer informar del primer siniestro por temor a que aumente el precio del seguro en el futuro - este comportamiento inflará la proporción de recuentos de cero. Ejemplos como estos últimos modifican la proporción de ceros. Es interesante mencionar que las modificaciones naturales de las tres distribuciones anteriores son capaces de proporcionar buenos ajustes a los conjuntos de datos cero modificados/truncados que se generan en el seguro.

Como se presenta a continuación, se modifica la probabilidad que se le asigna al valor cero en la clase \((a,b,0)\) manteniendo las probabilidades relativas asignadas a los valores no nulos - modificación en cero. Nótese que como la clase de distribuciones \((a,b,0)\) satisface la recurrencia (2.1), el mantenimiento de las probabilidades relativas de los valores no nulos implica que la recurrencia (2.1) se satisface para \(k\geq 2\). Esto nos lleva a la definición de la siguiente clase de distribuciones.

Definición. Una distribución de recuento es un miembro de la clase \((a, b, 1)\) si para las constantes \(a\) y \(b\) las probabilidades \(p_k\) satisfacen \[\begin{equation} \frac{p_k}{p_{k-1}}=a+\frac{b}{k},\quad k\geq 2. \tag{2.5} \end{equation}\]

Nótese que como la recursión empieza en \(p_1\), y no en \(p_0\), nos referimos a esta superclase de distribuciones \((a,b,0)\) como (a,b,1). Para entender esta clase, recordemos que cada par de valores válidos para \(a\) y \(b\) de la clase \((a,b,0)\) corresponde a un único vector de probabilidades \(\{p_k\}_{k\geq 0}\). Si ahora observamos el vector de probabilidades \(\{\tilde{p}_k\}_{k\geq 0}\) dado por

\[ \tilde{p}_k= \frac{1-\tilde{p}_0}{1-p_0}\cdot p_k, \quad k\geq 1, \]

donde \(\tilde{p}_0\in[0,1)\) se elige arbitrariamente, entonces como las probabilidades relativas de valores positivos de acuerdo con \(\{p_k\}_{k\geq 0}\) y \(\{\tilde{p}_k\}_{k\geq 0}\) son las mismas, tenemos que \(\{\tilde{p}_k\}_{k\geq 0}\) satisface la recurrencia (2.5). Esto, en particular, muestra que la clase de distribuciones \((a,b,1)\) es estrictamente más amplia que la \((a,b,0)\).

Previamente, hemos establecido un par de valores para \(a\) y \(b\) que llevaron a una distribución válida de \((a,b,0)\), y luego miramos las distribuciones \((a,b,1)\) que correspondían a esta distribución \((a,b,0)\). Ahora argumentaremos que la clase \((a,b,1)\) admite un conjunto mayor de distribuciones permitidas para \(a\) y \(b\) que la clase \((a,b,0)\). Recordemos de la Sección 2.3 que en el caso de \(a<0\) no se utiliza el hecho de que la recurrencia (2.1) empieza en \(k=1\), y por lo tanto el conjunto de pares \((a,b)\) con \(a<0\) que son admisibles para la clase \((a,b,0)\) es idéntico al que es admisible para la clase \((a,b,1)\). La misma conclusión se puede extraer fácilmente para los pares con \(a=0\). En el caso que \(a>0\), en lugar de la restricción \(a+b>0\) para la clase \((a,b,0)\), tenemos ahora la restricción más débil de \(a+b/2>0\) para la clase \((a,b,1)\). Con la parametrización \(b=(r-1)a\) utilizada en la Sección 2.3, en lugar de \(r>0\) tenemos ahora la restricción más débil de \(r>-1\). En particular, vemos que mientras que al modificar el cero en una distribución \((a,b,0)\) conduce a una distribución de la clase \((a,b,1)\), está conclusión no se cumple en la dirección contraria.

La modificación en cero de una distribución de recuento \(F\) tal que asigna una probabilidad cero al valor cero se llama un truncamiento en cero de \(F\). De este modo, la versión truncada en cero de las probabilidades \(\{p_k\}_{k\geq 0}\) viene dada por

\[ \tilde{p}_k=\begin{cases} 0, & k=0;\\ \frac{p_k}{1-p_0}, & k\geq 1. \end{cases} \]

En concreto, tenemos que una modificación en cero de una distribución de recuento \(\{p_k^T\}_{k\geq 0}\), denotada por \(\{p^M_k\}_{k\geq 0}\), puede escribirse como una combinación convexa de la distribución degenerada en \(0\) y el truncamiento en cero de \(\{p_k\}_{k\geq 0}\), denotado por \(\{p^T_k\}_{k\geq 0}\). De este modo tenemos

\[ p^M_k= p^M_0 \cdot \delta_{0}(k) + (1-p^M_0) \cdot p^T_k, \quad k\geq 0. \]

Ejemplo 2.5.1. Poisson Cero Modificada/Truncada. Considerar una distribución de Poisson con parámetro \(\lambda=2\). Calcular \(p_k, k=0,1,2,3\), para la usual (sin modificar), truncada y una versión modificada con \((p_0^M=0,6)\).

Mostrar Solución de Ejemplo

Solución. Para la distribución de Poisson como miembro de la clase ((\(a,b\),0), tenemos \(a=0\) y \(b=\lambda=2\). Por lo tanto, podemos usar para cada tipo la recursión \(p_k = \lambda p_{k-1}/k= 2 p_{k-1}/k\), después de determinar las probabilidades iniciales. El cálculo de probabilidades para \(k\leq 3\) se muestra en Tabla 2.2.

\[\begin{matrix} \begin{array}{c|c|c|c} \hline k & p_k & p_k^T & p_k^M\\\hline 0 & p_0=e^{-\lambda}=0,135335 & 0 & 0,6\\\hline 1 & p_1=p_0(0+\frac{\lambda}{1})=0,27067 & \frac{p_1}{1-p_0}=0,313035 & \frac{1-p_0^M}{1-p_0}~p_1=0,125214\\\hline 2 & p_2=p_1\left( \frac{\lambda}{2}\right)=0,27067 & p_2^T=p_1^T\left(\frac{\lambda}{2}\right)=0,313035 & p_2^M=p_1^M\left(\frac{\lambda}{2}\right)=0,125214\\\hline 3 & p_3=p_2\left(\frac{\lambda}{3}\right)=0,180447 & p_3^T=p_2^T\left(\frac{\lambda}{3}\right)=0,208690 & p_3^M=p_2^M\left(\frac{\lambda}{3}\right)=0,083476\\\hline \end{array} \end{matrix}\]

Tabla 2.2 : Cálculo de probabilidades para \(k\leq 3\)

---

2.6 Distribuciones Mixtas

---

En esta sección, se aprende a:

• Definir una distribución mixta cuando el componente de mixtura se basa en un número finito de subgrupos
• Calcular las probabilidades de la distribución mixta a partir de las proporciones de la mixtura y el conocimiento de la distribución de cada subgrupo
• Definir una distribución mixta cuando el componente de mixtura es continuo

---

En muchas aplicaciones la población subyacente consiste en subgrupos definidos de forma natural con cierta homogeneidad dentro de cada subgrupo. En estos casos es conveniente modelizar los subgrupos individuales y, de manera fundamentada, modelizar el conjunto de la población. Como veremos más adelante, más allá del atractivo del enfoque, también se amplía el abanico de aplicaciones que pueden cubrirse mediante las distribuciones paramétricas estándar.

Supongamos que \(k\) denota el número de subgrupos definidos en una población, y \(F_i\) denota la distribución de una observación extraída del subgrupo \(i\)-ésimo. Si dejamos que \(\alpha_i\) denote la proporción de la población en el subgrupo \(i\)-ésimo, con \(\sum_{i=1}^k \alpha_i=1\), entonces la distribución de una observación elegida al azar de la población, denotada por \(F\), viene dada por

\[\begin{equation} F(x)=\sum_{i=1}^k \alpha_i \cdot F_i(x). \tag{2.6} \end{equation}\]

La expresión anterior puede considerarse una aplicación directa de la Ley de Probabilidad Total. Como ejemplo, consideremos una población de conductores dividida en dos subgrupos, los que tienen como máximo \(5\) años de experiencia de conducción y los que tienen más de \(5\) años de experiencia. Supongamos que \(\alpha\) denota la proporción de conductores con menos de \(5\) años de experiencia, y \(F_{\leq 5}\) y \(F_{> 5}\) denotan la distribución del número de siniestros en un año para un conductor de cada grupo, respectivamente. Entonces la distribución del número de siniestros de un conductor seleccionado al azar viene dada por

\[ \alpha\cdot F_{\leq 5}(x) + (1-\alpha)F_{> 5}(x). \]

Una definición alternativa de una distribución mixta es la siguiente. Supongamos que \(N_i\) es una variable aleatoria con distribución \(F_i\), \(i=1,\ldots, k\). Sea \(I\) una variable aleatoria que toma valores \(1,2,\ldots,k\) con probabilidades \(\alpha_1,\ldots,\alpha_k\), respectivamente. Entonces, la variable aleatoria \(N_I\) tiene una distribución dada por la ecuación (2.6)⁸.

En (2.6) vemos que la función de distribución es una combinación convexa de las funciones de distribución que la componen. Este resultado se extiende fácilmente a la función de densidad, la función de supervivencia, los momentos ordinarios y el valor esperado, ya que todos ellos son aplicaciones lineales de la función de distribución. Observamos que esto no es cierto en el caso de los momentos centrales como la varianza, y de las medidas condicionales como la función de tasa de riesgo (hazard rate). En el caso de la varianza se ve fácilmente como

\[\begin{equation} \mathrm{Var}{[N_I]}=\mathrm{E}[{\mathrm{Var}[{N_I\vert I}]]} + \mathrm{Var}[{\mathrm{E}[{N_I|I}}]]=\sum_{i=1}^k \alpha_i \mathrm{Var}[{N_i}] + \mathrm{Var}[{\mathrm{E}[{N_I|I}}]] . \tag{2.7} \end{equation}\]

El Apéndice 16 proporciona información adicional sobre esta importante expresión.

Ejemplo 2.6.1. Pregunta de Examen Actuarial. En una determinada ciudad el número de resfriados comunes que un individuo tendrá en un año sigue una distribución de Poisson que depende de la edad del individuo y su condición de fumador. La distribución de la población y el número medio de resfriados son los siguientes:

\[\begin{matrix} \begin{array}{l|c|c} \hline & \text{Proporción de población} & \text{Número medio de resfriados}\\\hline \text{Niños} & 0,3 & 3\\ \text{Adultos No-fumadores} & 0,6 & 1\\ \text{Adultos Fumadores} & 0,1 & 4\\\hline \end{array} \end{matrix}\]

Tabla 2.3 : La distribución de la población y el número medio de resfriados

1. Calcular la probabilidad de que una persona seleccionada al azar tenga 3 resfriados comunes en un año.
2. Calcular la probabilidad condicionada de que una persona con exactamente 3 resfriados comunes en un año sea un fumador adulto.

Mostrar Solución de Ejemplo

Solución.

1. Utilizando la Ley de Probabilidad Total, podemos escribir la probabilidad requerida como \(\Pr(N_I=3)\), con \(I\) que denota el grupo del individuo seleccionado al azar con \(1,2\) y \(3\) que significan los grupos Niños, Adulto No Fumador, y Adulto Fumador, respectivamente. Ahora, por el condicionamiento, tenemos \[ \Pr(N_I=3)=0,3\cdot\Pr(N_1=3)+0,6\cdot\Pr(N_2=3)+0,1\cdot\Pr(N_3=3), \] con \(N_1,N_2\) y \(N_3\) que siguen una distribución de Poisson de media \(3,1\), y \(4\), respectivamente. Utilizando lo anterior, obtenemos \(\Pr(N_I=3)\sim0,1235\)

2. La probabilidad condicionada del evento A dado el evento B, \(\Pr(A\vert B) = \frac{\Pr(A,B)}{\Pr(B)}\). La probabilidad condicionada requerida en este problema puede escribirse como \(\Pr(I=3\vert N_I=3)\), que es igual a

\[ \Pr(I=3\vert N_I=3)=\frac{\Pr(I=3,N_3=3)}{\Pr(N_I=3)}\sim\frac{0,1 \times 0,1954}{0,1235}\sim 0,1581. \]

---

En el ejemplo previo, el número de subgrupos \(k\) era igual a tres. En general, \(k\) puede ser cualquier número natural, pero cuando \(k\) es grande es parsimonioso desde el punto de vista de la modelización tomar el siguiente enfoque de infinitamente muchos subgrupos. Para justificar este enfoque, supongamos que el subgrupo \(i\)-ésimo sea tal que su distribución componente \(F_i\) viene dada por \(G_{\tilde{\theta_i}}\), donde \(G_\cdot\) es una familia paramétrica de distribuciones con espacio paramétrico \(\Theta\subseteq \mathbb{R}^d\). Con este supuesto, la función de distribución \(F\) de una observación extraída aleatoriamente de la población viene dada por

\[ F(x)=\sum_{i=1}^k \alpha_i G_{\tilde{\theta_i}}(x),\quad \forall x\in\mathbb{R}. \] que puede escribirse alternativamente como \[ F(x)=\mathrm{E}[{G_{\tilde{\vartheta}}(x)}],\quad \forall x\in\mathbb{R}, \] donde \(\tilde{\vartheta}\) toma valores \(\tilde{\theta_i}\) con probabilidad \(\alpha_i\), para \(i=1,\ldots,k\). Esto muestra que cuando \(k\) es grande, se puede modelizar lo anterior tratando \(\tilde{\vartheta}\) como una variable aleatoria continua.

Para ilustrar este enfoque, supongamos que tenemos una población de conductores con la distribución de siniestros de un conductor individual que se distribuye como una Poisson. Cada persona tiene su propio (personal) número esperado de siniestros \(\lambda\) - valores más pequeños para los buenos conductores, y valores más grandes para el resto. Hay una distribución de \(\lambda\) en la población; una opción común y conveniente para la modelización de esta distribución es una distribución gamma con parámetros \((\alpha, \theta)\). Con estas características resulta que la distribución resultante de \(N\), los siniestros de un conductor elegido aleatoriamente, es una binomial negativa con parámetros \((r=\alpha,\beta=\theta)\). Esto puede mostrarse de muchas maneras, pero una forma sencilla es la siguiente:

\[\begin{align*} \Pr(N=k)&= \int_0^\infty \frac{e^{-\lambda}\lambda^k}{k!} \frac{\lambda^{\alpha-1}e^{-\lambda/\theta}}{\Gamma{(\alpha)}\theta^{\alpha}} {\rm d}\lambda = \frac{1}{k!\Gamma(\alpha)\theta^\alpha}\int_0^\infty \lambda^{\alpha+k-1}e^{-\lambda(1+1/\theta)}{\rm d}\lambda=\frac{\Gamma{(\alpha+k)}}{k!\Gamma(\alpha)\theta^\alpha(1+1/\theta)^{\alpha+k}} \\ &=\binom{\alpha+k-1}{k}\left(\frac{1}{1+\theta}\right)^\alpha\left(\frac{\theta}{1+\theta}\right)^k, \quad k=0,1,\ldots \end{align*}\] Obsérvese que la derivación previa utiliza implícitamente lo siguiente: \[ f_{N\vert\Lambda=\lambda}(N=k)=\frac{e^{-\lambda}\lambda^k}{k!}, \quad k\geq 0; \quad \hbox{y} \quad f_{\Lambda}(\lambda)= \frac{\lambda^{\alpha-1}e^{-\lambda/\theta}}{\Gamma{(\alpha)}\theta^{\alpha}}, \quad \lambda>0. \]

Cabe mencionar que al considerar las mixturas de una clase paramétrica de distribuciones se incrementa la riqueza de la clase. Esta expansión de las distribuciones da como resultado que la clase de mixtura pueda adaptarse bien a más aplicaciones que la clase paramétrica inicial. La modelización de mixturas es una técnica de modelización muy importante en las aplicaciones de seguros, y en los capítulos posteriores se tratarán más aspectos de esta técnica de modelización.

Ejemplo 2.6.2. Supongamos que \(N|\Lambda \sim\) Poisson\((\Lambda)\) y que \(\Lambda \sim\) gamma con media de 1 y varianza de 2. Determinar la probabilidad que \(N=1\).

Mostrar Solución de Ejemplo

Solución. Para una distribución gamma con parámetros \((\alpha, \theta)\), tenemos que la media es \(\alpha \theta\) y la varianza es \(\alpha \theta^2\). En base a estas expresiones tenemos que \[ \begin{aligned} \alpha &= \frac{1}{2} \text{ y } \theta =2. \end{aligned} \] Ahora, se puede utilizar directamente el resultado anterior para concluir que \(N\) se distribuye como una binomial negativa con \(r = \alpha = \frac{1}{2}\) y \(\beta= \theta =2\). Por lo tanto, \[ \begin{aligned} \Pr(N=1) &= \binom{1+r-1}{1}(\frac{1}{(1+\beta)^r})\left(\frac{\beta}{1+\beta}\right)^1 \\ &= \binom{1+\frac{1}{2}-1}{1}{\frac{1}{(1+2)^{1/2}}}\left(\frac{2}{1+2}\right)^1\\ &= \frac{1}{3^{3/2}} = 0,19245 . \end{aligned} \]

---

2.7 Bondad del Ajuste

---

En esta sección, se aprende a:

• Calcular un estadístico de bondad del ajuste para comparar una distribución discreta hipotética con una muestra de observaciones discretas
• Comparar el estadístico con una distribución de referencia para evaluar la adecuación del ajuste

---

Previamente se han analizado tres distribuciones de frecuencias elementales, junto con sus extensiones mediante la modificación/truncamiento en cero y mostrando las mixturas de estas distribuciones. Ahora bien, estas clases siguen siendo paramétricas y, por tanto, por su propia naturaleza, un pequeño subconjunto de la clase de todas las distribuciones de frecuencia posibles (i.e. el conjunto de distribuciones para números enteros no negativos.) Por lo tanto, aunque hemos mostrado métodos para estimar los parámetros desconocidos, la distribución ajustada no será una buena representación de la distribución subyacente si ésta está lejos de la clase de distribución utilizada en la modelización. De hecho, se puede demostrar que el estimador máximo verosímil convergerá a un valor de tal forma que la distribución correspondiente será una proyección Kullback-Leibler de la distribución subyacente en la clase de distribuciones utilizada para la modelización. A continuación presentamos un método de contraste - el estadístico chi-cuadrado de Pearson - para comprobar la bondad del ajuste de la distribución ajustada. Para más detalles sobre el contraste chi-cuadrado de Pearson, a un nivel introductorio de estadística matemática, remitimos al lector a la Sección 9.1 de (Hogg, Tanis, and Zimmerman 2015).

En \(1993\), una cartera de \(n=7.483\) pólizas de seguro de automóvil de una importante compañía de seguros de Singapur tenía la distribución de accidentes de automóvil por asegurado como se indica en Tabla 2.4.

\[\begin{matrix} \begin{array}{c|c|c|c|c|c|c} \hline \text{Número }(k) & 0 & 1 & 2 & 3 & 4 & \text{Total}\\ \hline \text{No. de Pólizas con }k\text{ accidentes }(m_k) & 6.996 & 455 & 28 & 4 & 0 & 7483\\ \hline \end{array} \end{matrix}\]

Tabla 2.4 : Datos de Accidentes de Automóvil en Singapur

Si se ajusta una distribución de Poisson, entonces el MLE para \(\lambda\), la media de la Poisson, es la media muestral que es igual a \[ \overline{N} = \frac{0\cdot 6996 + 1 \cdot 455 + 2 \cdot 28 + 3 \cdot 4 + 4 \cdot 0}{7483} = 0,06989. \] Ahora si se usa la Poisson (\(\hat{\lambda}_{MLE}\)) como la distribución ajustada, entonces una comparación tabular de los valores ajustados y los valores observados se muestra en la Tabla 2.5 siguiente, donde \(\hat{p}_k\) representa las probabilidades estimadas mediante la distribución de Poisson ajustada.

\[\begin{matrix} \begin{array}{c|c|c} \hline \text{Número} & \text{Observado} & \text{Ajustado}\\ (k) & (m_k) & \text{Usando Poisson }(n\hat{p}_k)\\ \hline 0 & 6.996 & 6.977,86 \\ 1 & 455 & 487,70 \\ 2 & 28 & 17,04 \\ 3 & 4 & 0,40 \\ \geq4 & 0 & 0,01\\ \hline \text{Total} & 7.483 & 7.483,00\\ \hline \end{array} \end{matrix}\]

Tabla 2.5 : Comparación entre valores observados y ajustados: Datos de automóviles de Singapur

Mientras que el ajuste parece razonable, una comparación tabular no es suficiente como contraste estadístico de la hipótesis de que la distribución subyacente es efectivamente la Poisson. El estadístico de chi-cuadrado de Pearson es una medida de bondad del ajuste que puede utilizarse para este propósito. Para explicar este estadístico, supongamos que un conjunto de datos de tamaño \(n\) se agrupa en \(k\) celdas, siendo \(m_k/n\) y \(\hat{p}_k\), para \(k=1\ldots,K\), las probabilidades observadas y estimadas de que una observación pertenezca a la celda \(k\)-ésima, respectivamente. El estadístico del contraste chi-cuadrado de Pearson viene dado por

\[ \sum_{k=1}^K\frac{\left( m_k-n\widehat{p}_k \right) ^{2}}{n\widehat{p}_k}. \] La justificación del estadístico anterior se deriva del hecho que

\[ \sum_{k=1}^K\frac{\left( m_k-n{p}_k \right) ^{2}}{n{p}_k} \]

tiene como límite una distribución chi-cuadrado con \(K-1\) grados de libertad si \(p_k\), \(k=1,\ldots,K\) son las probabilidades verdaderas de cada celda. Ahora supongamos que sólo los datos resumidos representados por \(m_k\), \(k=1,\ldots,K\) están disponibles. Además, si las \(p_k\) son funciones de \(s\) parámetros, sustituyendo las \(p_k\) por cualquier probabilidad estimada eficientemente \(\widehat{p}_k\), el estadístico sigue teniendo una distribución chi-cuadrado como límite pero con \(K-1-s\) grados de libertad. Estas estimaciones eficientes pueden obtenerse, por ejemplo, usando el método MLE (con una verosimilitud multinomial) o estimando los \(s\) parámetros que minimizan el estadístico chi-cuadrado de Pearson previo. Por ejemplo, el código R que se muestra a continuación realiza una estimación de \(\lambda\) en base a esto último y se obtiene un estimador de \(0,06623153\), cercano pero diferente del MLE de \(\lambda\) usando la totalidad de los datos:

m<-c(6996,455,28,4,0);
op<-m/sum(m);
g<-function(lam){sum((op-c(dpois(0:3,lam),1-ppois(3,lam)))^2)};
optim(sum(op*(0:4)),g,method="Brent",lower=0,upper=10)$par

Cuando se usa la totalidad de los datos para estimar las probabilidades, la distribución asintótica está entre las distribuciones chi-cuadrado con parámetros \(K-1\) y \(K-1-s\). En la práctica, normalmente no se considera este matiz y se asume que la chi-cuadrado límite tiene \(K-1-s\) grados de libertad. Curiosamente, esta forma de actuar funciona bastante bien en el caso de la distribución de Poisson.

Para los datos de autos de Singapur el estadístico chi-cuadrado de Pearson es igual a \(41,98\) utilizando el conjunto de datos MLE para \({\lambda}\). Usando la distribución límite de chi-cuadrado con \(5-1-1=3\) grados de libertad, vemos que el valor de \(41,98\) está muy lejos en la cola (el percentil \(99\) está por debajo de \(12\)). Por lo tanto, podemos concluir que la distribución de Poisson proporciona un ajuste inadecuado para los datos.

Anteriormente, en la tabla resumen previa hemos considerado que las celdas vienen dadas. En la práctica, una pregunta relevante es cómo definir las celdas para que la distribución chi-cuadrado sea una buena aproximación a la distribución de muestra finita del estadístico. Una regla empírica es definir las celdas de tal manera que el \(80%\) de las celdas, si no todas, tengan al menos valores esperados mayores a \(5\). Además, puesto que un mayor número de celdas proporciona una mayor potencia del contraste, una simple regla empírica es por tanto maximizar el número de celdas de tal forma que cada celda tenga al menos 5 observaciones.

2.8 Ejercicios

Ejercicios Teóricos

Ejercicio 2.1. Derivar una expresión para \(p_N(\cdot)\) en términos de \(F_N(\cdot)\) y \(S_N(\cdot)\).

Ejercicio 2.2. Una medida del centro de localización debe ser equivariable con respecto a los desplazamientos, o transformaciones de localización. En otras palabras, si \(N_1\) y \(N_2\) son dos variables aleatorias tales que \(N_1+c\) tiene la misma distribución que \(N_2\), para una constante \(c\), entonces la diferencia entre las medidas del centro de localización de \(N_2\) y \(N_1\) debe ser igual a \(c\). Mostrar que la media satisface esta propiedad.

Ejercicio 2.3. Las medidas de dispersión deben ser invariables con respecto a desplazamientos y escala equi-variables. Demuestre que la desviación estándar satisface estas propiedades haciendo lo siguiente:

• Mostrar que para una variable aleatoria \(N\), su desviación estándar es igual a la de \(N+c\), para cualquier constante \(c\).
• Mostrar que para una variable aleatoria \(N\), su desviación estándar es igual a \(1/c\) por \(cN\), para cualquier constante positiva \(c\).

Ejercicio 2.4. Supongamos que \(N\) es una variable aleatoria con función masa de probabilidad dada por \[ p_N(k):= \begin{cases} \left(\frac{6}{\pi^2}\right)\left(\frac{1}{k^{2}}\right), & k\geq 1;\\ 0, &\hbox{en otro caso}. \end{cases} \] Demostrar que la media de \(N\) es \(\infty\).

Ejercicio 2.5. Supongamos que \(N\) es una variable aleatoria con segundo momento finito. Demostrar que la función \(\psi(\cdot)\) definida por \[ \psi(x):=\mathrm{E}{(N-x)^2}. \quad x\in\mathbb{R} \] se minimiza en \(\mu_N\) sin realizar cálculos. También, proporcionar una demostración de este resultado mediante derivadas. Concluir que el valor mínimo es igual a la varianza de \(N\).

Ejercicio 2.6. Derivar los dos primeros momentos centrales de las distribuciones \((a,b,0)\) utilizando los métodos mencionados a continuación:

• Para la distribución binomial, derivar los momentos usando sólo su pmf, luego su mgf, y luego su pgf.
• Para la distribución Poisson, derivar los momentos usando sólo su mgf.
• Para la distribución binomial negativa, derivar los momentos usando sólo su pmf, y luego su pgf.

Ejercicio 2.7. Supongamos que \(N_1\) y \(N_2\) son dos variables aleatorias independientes de Poisson con medias \(\lambda_1\) y \(\lambda_2\), respectivamente. Identificar la distribución condicionada de \(N_1\) dado \(N_1+N_2\).

Ejercicio 2.8. (No unicidad de MLE)

Considerar la siguiente familia paramétrica de densidades indexadas por el parámetro \(p\) que toma valores en \([0,1]\): \[ f_p(x)=p\cdot\phi(x+2)+(1-p)\cdot\phi(x-2), \quad x\in\mathbb{R}, \] donde \(\phi(\cdot)\) representa la densidad normal estándar.

• Mostrar que para todos los \(p\in[0,1]\), la \(f_p(\cdot)\) previa es una función de densidad válida.
• Encontrar una expresión en \(p\) para la media y la varianza de \(f_p(\cdot)\).
• Supongamos una muestra de tamaño uno que consiste en \(x\). Mostrar que cuando \(x\) es igual a \(0\), el conjunto de estimadores máximo verosímiles para \(p\) es igual a \([0,1]\); también mostrar que el MLE es único en otro caso.

Ejercicio 2.9. Representar gráficamente la región del plano que corresponde a los valores de \((a,b)\) que dan lugar a distribuciones \((a,b,0)\) válidas. Hacer lo mismo para las distribuciones \((a,b,1)\).

Ejercicio 2.10. (Complejidad computacional) Para la clase de distribuciones \((a,b,0)\), contabilizar el número de operaciones matemáticas básicas (suma, resta, multiplicación, división) necesarias para calcular las \(n\) probabilidades \(p_0\ldots p_{n-1}\) utilizando la relación de recurrencia. Para la distribución binomial negativa con \(r\) no entero, contabilizar el número de estas operaciones. ¿Qué es lo que observas?

Ejercicio 2.11. (** **) Utilizando el desarrollo de la Sección 2.3 mostrar de forma rigurosa que no sólo la recurrencia (2.1) une las distribuciones binomiales, Poisson y binomial negativa, sino que también las caracteriza.

Ejercicios con Enfoque Práctico

Ejercicio 2.12. Pregunta de Examen Actuarial. Se conoce:

1. \(p_k\) denota la probabilidad que el número de siniestros sea igual a \(k\) para \(k=0,1,2,\ldots\)
2. \(\frac{p_n}{p_m}=\frac{m!}{n!}, m\ge 0, n\ge 0\)

Usando la distribución correspondiente del número de siniestros cero-modificada con \(p_0^M=0,1\), calcular \(p_1^M\).

Ejercicio 2.13. Pregunta de Examen Actuarial. Durante un período de un año, el número de accidentes por día se distribuyó de la siguiente manera:

\[ \begin{matrix} \begin{array}{c|c|c|c|c|c|c} \hline \text{No. de Accidentes} & 0 & 1 & 2 & 3 & 4 & 5\\ \hline \text{No. de Días} & 209 & 111 & 33 & 7 & 5 & 2\\ \hline \end{array} \end{matrix} \]

Se utiliza un contraste chi-cuadrado para medir el ajuste de una distribución de Poisson con una media de 0,60. El número mínimo esperado de observaciones en cualquier grupo debe ser 5. El número máximo de grupos debe utilizarse. Determinar el valor del estadístico chi-cuadrado.

Ejercicio 2.14. Una distribución de probabilidad discreta tiene las siguientes propiedades \[ \begin{aligned} \Pr(N=k) = \left( \frac{3k+9}{8k}\right) \Pr(N=k-1), \quad k=1,2,3,\ldots \end{aligned} \] Determinar el valor de \(\Pr(N=3)\). (Resp: 0,1609)

Ejercicios Adicionales

Aquí se encuentra un conjunto de ejercicios que guían al lector a través de algunos de los fundamentos teóricos de Loss Data Analytics. Cada tutorial se basa en una o más preguntas de los exámenes actuariales profesionales - normalmente el examen C de la Society of Actuaries.

Tutoriales Guiados de Distribución de Frecuencias

2.9 Recursos Adicionales y Autores

El Capítulo del Apéndice 15 ofrece una introducción general a la teoría de máxima verosimilitud en relación con la estimación de los parámetros de una familia paramétrica. El Capítulo del Apéndice 17 proporciona ejemplos más específicos y expande algunos de los conceptos.

Autoría

• N.D. Shyamalkumar, The University of Iowa, y Krupa Viswanathan, Temple University, son los autores principales de la versión inicial de este capítulo. Email: shyamal-kumar@uiowa.edu para comentarios del capítulo y sugerencias de mejora.

• Revisores del Capítulo incluyen: Paul Johnson, Hirokazu (Iwahiro) Iwasawa, Rajesh Sahasrabuddhe, Michelle Xia.

• Traducción al español: Ramon Alemany y Miguel Santolino (Universitat de Barcelona).

2.9.1 TS 2.A. Código R para Gráficos

Código para Figura 2.3:

Mostrar Código R

likbinm<-function(m){ 
  # verosimilitud binomial maximizada con respecto a p
  prod((dbinom(x,m,mean(x)/m)))
}

liknbinm<-function(r){
  # verosimilitud binomial negativa maximizada con respecto a beta
  prod(dnbinom(x,r,1-mean(x)/(mean(x)+r)))
}

# Datos Matriciales; Tres muestras, una en cada Columna; 
# Primera Muestra tiene Var<Mean
# Segunda Muestra tiene Var=Mean
# Tercera Muestra tiene Var>Mean

  X<-cbind(c(2,5,6,8,9)+2,c(2,5,6,8,9),c(2,3,6,8,9)); 

# Se utiliza para crear las etiquetas en la matriz z 
 ord_char<-c("<","=",">"); 
  
# Matrices vacías; 
  Y<-matrix(1,ncol=2,nrow=0); 
  Z<-matrix(1,ncol=2,nrow=0); 

for (i in (1:3)) {
  # Trabaja con los datos de la i-ésima muestra 
   x<-X[,i]; 
  
  # Verosimilitud Binomial
      # Intervalo de n valores cubriendo la MLE
        n<-(9:100);
      # Evaluación de la verosimilitud en varios valores de n
        ll<-sapply(n,likbinm); 
      # Encontrando la MLE de n
        n[ll==max(ll[!is.na(ll)])] 
      # Almacenamiento de los datos y las etiquetas
        Y<-rbind(Y,cbind(n,ll));
        Z<-rbind(Z,cbind(rep(paste("$\\hat{\\sigma}^2",ord_char[i],"\\hat{\\mu}$"),length(n)),rep("Binomial - $L(m,\\overline{x}/m)$",length(n))));

  # Verosimilitud Binomial Negativa
    # Intervalo de valores de r 
      r<-(1:100);
    # Evaluación de la verosimilitud en varios valores de r
      ll<-sapply(r,liknbinm); 
    # Encontrando la MLE de r
      ll[is.na(ll)]=0;
      r[ll==max(ll[!is.na(ll)])]; 
    # Almacenamiento de los datos y las etiquetas
      Y<-rbind(Y,cbind(r,ll));
      Z<-rbind(Z,cbind(rep(paste("$\\hat{\\sigma}^2",ord_char[i],"\\hat{\\mu}$"),length(r)),rep("Neg.Binomial - $L(r,\\overline{x}/r)$",length(r))));
      
  # Verosimilitud de Poisson
    # Almacenamiento de los datos y las etiquetas
    # En el caso de la Poisson la MLE es la media muestral
      Y<-rbind(Y,cbind(r,rep(prod(dpois(x,mean(x))),length(r))));
      Z<-rbind(Z,cbind(rep(paste("$\\hat{\\sigma}^2",ord_char[i],"\\hat{\\mu}$"),length(r)),rep("Poisson - $L(\\overline{x})$",length(r))));
}

  # Asignación de Nombres a las Columnas
    colnames(Y)<-c("x","lik");
    colnames(Z)<-c("dataset","Distribution");
  # Creación de un Dataframe para usar ggplot
    dy<-cbind(data.frame(Y),data.frame(Z));


library(tikzDevice);
library(ggplot2);
options(tikzMetricPackages = c("\\usepackage[utf8]{inputenc}","\\usepackage[T1]{fontenc}", "\\usetikzlibrary{calc}", 
                               "\\usepackage{amssymb}","\\usepackage{amsmath}","\\usepackage[active]{preview}"))
tikz(file = "plot_test_2.tex", width = 6.25, height = 6.25);
ggplot(data=dy,aes(x=x,y=lik,col=Distribution)) + geom_point(size=0.25) + facet_grid(dataset~.)+
  labs(x="m/r",y="Verosimilitud",title=""); 
dev.off();

---

Código para Figura 2.2:

Mostrar Código de R

likm<-function(m){
  prod((dbinom(x,m,mean(x)/m)))
}
x<-c(2,2,2,4,5);
n<-(5:100);
# Cálculo de la verosimilitud 
ll<-sapply(n,likm); 
# Calculando MLE
n[ll==max(ll)]
# Almacenamiento de la curva de verosimilitud
y<-cbind(n,ll);

# Segundo conjunto de datos
x<-c(2,2,2,4,6);
ll<-sapply(n,likm);
n[ll==max(ll)]
y<-cbind(y,ll);

# Tercer conjunto de datos
x<-c(2,2,2,4,7);
ll<-sapply(n,likm);
n[ll==max(ll)]
y<-cbind(y,ll);

colnames(y)<-c("m","$\\tilde{x}=(2,2,2,4,5)$","$\\tilde{x}=(2,2,2,4,6)$","$\\tilde{x}=(2,2,2,4,7)$");
dy<-data.frame(y);
library(tikzDevice);
library(ggplot2);
options(tikzMetricPackages = c("\\usepackage[utf8]{inputenc}","\\usepackage[T1]{fontenc}", "\\usetikzlibrary{calc}", 
                               "\\usepackage{amssymb}","\\usepackage{amsmath}","\\usepackage[active]{preview}"))
tikz(file = "plot_test.tex", width = 6.25, height = 3.125);
ggplot(dy) + 
  geom_point(aes(x=m, y=(X..tilde.x...2.2.2.4.5..),shape="$\\tilde{x}=(2,2,2,4,5):\\hat{m}=7$"),size=0.75) + 
  geom_point(aes(x=m, y=(X..tilde.x...2.2.2.4.6..),shape="$\\tilde{x}=(2,2,2,4,6):\\hat{m}=18$"),size=0.75) +
  geom_point(aes(x=m, y=(X..tilde.x...2.2.2.4.7..),shape="$\\tilde{x}=(2,2,2,4,7):\\hat{m}=\\infty$"),size=0.75) +
  geom_point(aes(x=c(7),y=dy$X..tilde.x...2.2.2.4.5..[3],colour="$\\hat{m}$",shape="$\\tilde{x}=(2,2,2,4,5):\\hat{m}=7$"),size=0.75)+
  geom_point(aes(x=c(18),y=dy$X..tilde.x...2.2.2.4.6..[14],colour="$\\hat{m}$",shape="$\\tilde{x}=(2,2,2,4,6):\\hat{m}=18$"),size=0.75)+
  labs(x="m",y="$L(m,\\overline{x}/m)$",title="MLE para $m$: No-Robustez de MLE "); 
dev.off();

---

Bibliography

Billingsley, Patrick. 2008. Probability and Measure. John Wiley & Sons.

Frees, Edward W. 2009. Regression Modeling with Actuarial and Financial Applications. Cambridge University Press.

Hogg, Robert V, Elliot A Tanis, and Dale L Zimmerman. 2015. Probability and Statistical Inference, 9th Edition. Pearson, New York.

Levin, Bruce, James Reeds, and others. 1977. “Compound Multinomial Likelihood Functions Are Unimodal: Proof of a Conjecture of Ij Good.” The Annals of Statistics 5 (1): 79–87.

Olkin, Ingram, A John Petkau, and James V Zidek. 1981. “A Comparison of N Estimators for the Binomial Distribution.” Journal of the American Statistical Association 76 (375): 637–42.

---

2. Por comodidad, indexamos \(\mu_N\) con la variable aleatoria \(N\) en lugar de \(F_N\) o \(p_N\), aunque es una función de la distribución de la variable aleatoria.↩

3. \(0^0 = 1\)↩

4. A partir de aquí suprimiremos la referencia a \(N\) y denotaremos la pmf por la secuencia \(\{p_k\}_{k\geq 0}\), en vez de la función \(p_N(\cdot)\).↩

5. Para la base teórica que subyace de la expresión anterior, ver (Billingsley 2008).↩

6. El conjunto de maximizadores de \(L(\cdot)\) son los mismos que el conjunto de maximizadores de cualquier función estrictamente creciente de \(L(\cdot)\), y por lo tanto son los mismos que los de \(l(\cdot)\).↩

7. Una pequeña ventaja de trabajar con \(l(\cdot)\) es que los términos constantes en \(L(\cdot)\) no aparecen en \(l'(\cdot)\) mientras que si lo hacen en \(L'(\cdot)\).↩

8. Esto, en concreto, establece una forma de simular a partir de una distribución mixta que hace uso de los eficientes esquemas de simulación que pueden existir para las distribuciones que la componen.↩