Chapter 7 Fundamentos de la Prima
Resumen del capítulo. Definir los precios para los productos aseguradores, las primas, es una tarea importante para los actuarios y otros analistas de datos. Este capítulo introduce las bases o fundamentos para tarificar productos de no-vida.
7.1 Introducción a la Tarificación
En esta sección, se aprende cómo:
- Definir la esperanza matemática como referencia del método para determinar las primas del seguro
- Analizar una ecuación contable para relacionar primas con siniestros, gastos y beneficios
- Resumir la estrategia para extender la tarificación en caso de riesgos heterogéneos y tendencias temporales
Este capítulo explica cómo podemos pensar en determinar el precio apropiado para un producto asegurador. Como se describe en la Sección 1.2, una función actuarial clave es la tarificación, donde el analista busca determinar el precio correcto para un riesgo.
Siendo ésta una función clave, empecemos por dar un paso atrás y definir algunos términos. Un precio es una cantidad, normalmente de dinero, que es intercambiada por un producto o un servicio. En seguros, normalmente utilizamos la palabra prima como la cantidad de dinero cobrada por la protección aseguradora ante acontecimientos inciertos. La cantidad de protección varía según el riesgo asegurado. Por ejemplo, en un seguro del hogar, la cantidad de la protección del seguro depende del valor de la casa. En un seguro de vida, la cantidad de protección depende del estado financiero (p. ej. ingresos y riqueza) del asegurado, así como de la necesidad percibida para su seguridad financiera. En consecuencia, es común expresar el precio del seguro como una unidad de la protección que está siendo adquirida, por ejemplo, una cantidad en miles (p. ej., de dólares o Euros) para la cobertura de una casa o del pago acordado en caso de muerte. Como estos/as precios/primas están expresados/as en unidades estandarizadas, también se denominan como tarifas.
Para determinar precios, en economía, es común considerar la oferta y la demanda de un producto. La demanda es sensible al precio y a la existencia de empresas en competencia o de productos alternativos. La oferta viene determinada en función de los recursos necesarios para la producción. Para una empresa individual, el precio estará definido para cumplir con el objetivo de maximizar su beneficio, lo que conseguirá escogiendo el nivel de producción que equilibre los costes y los ingresos al nivel de margen deseado.
Sin embargo, una peculiaridad del seguro es que los costes de la protección aseguradora no son conocidos en el momento de la venta del contrato. Si el acontecimiento incierto asegurado, como la pérdida de una casa o la vida, no ocurre, entonces los costes de contrato son sólo administrativos (para formalizar el contrato) y son relativamente menores. Si el acontecimiento asegurado ocurre, entonces el coste incluye no sólo los costes administrativos sino también el pago de la cantidad asegurada y los gastos para gestionar la reclamación. Por lo tanto, el coste es aleatorio cuando el contrato se formaliza: por diseño del producto, ni asegurador ni asegurado conocen los costes de contrato. Además, los costes pueden no ser revelados en meses o años. Por ejemplo, un tiempo normal para la liquidación de una mala práctica médica es de cinco años.
Al ser desconocidos los costes en el momento de la venta, la determinación del precio del seguro difiere de las aproximaciones económicas comunes.
Este capítulo aborda decididamente la naturaleza incierta de los costes mediante aproximaciones actuariales tradicionales que determinan los precios en función de los costes del seguro. Como veremos, esta aproximación de tarificación es suficiente para algunos ramos de seguro, como automóvil o hogar, donde el asegurador tiene una cartera de muchos riesgos independientes. Sin embargo, existen otros ramos de seguro donde los precios actuariales sólo proporcionan un dato más para los precios generales del mercado. Para reforzar esta distinción, las primas basadas en el coste actuarial son a veces denominadas como precios técnicos. Desde la perspectiva de los economistas, algunas decisiones corporativas como la tarificación deben ser evaluadas teniendo en cuenta su impacto en el valor de mercado de la empresa. Este objetivo es más completo que la idea estática de la maximización del beneficio. Esto es, asumiendo que el valor de la empresa representa el valor actualizado de todos los beneficios esperados en el futuro. Las decisiones que impactan en este valor afectan a todos aquellos grupos que pueden reclamar a la empresa, incluyendo accionistas, obligacionistas, asegurados (en el caso de las mutuas de seguros), y otros.
<!—Dado que los costes no son conocidos en el momento de la venta del seguro, este capítulo se centra, siguiendo la literatura actuarial, en los costes de ofrecer un seguro. Esta no será una visión completa de todo lo necesario para determinar el precio del seguro. –>
Para los precios basados en costes, es útil pensar en la prima como fuente de ingresos necesaria para hacer frente a los pagos de los siniestros y los gastos operativos, y además, obtener un margen de beneficio. Podemos formalizar esto en la siguiente ecuación contable
\[\begin{equation} \small{ \text{Prima = Siniestros + Gastos + Margen Beneficio} . } \tag{7.1} \end{equation}\]
Los gastos pueden ser divididos entre aquellos que varían según la prima (como las comisiones por ventas) y los que no (como los costes de gestión y los salarios de los empleados). El término Margen Beneficio es la parte residual que representa el beneficio por suscripción (underwriting benefit, en inglés). También puede incluir el coste de capital (por ejemplo, el dividendo anual a los inversores de la compañía). Como estos gastos fijos y costes de capitales son difícilmente interpretables al nivel de los contratos individuales, pensamos en la igualdad de la ecuación (7.1) como aquella existente sobre la suma de muchos contratos (una cartera) y trabajamos con ella a nivel agregado o conjunto. De este modo, en la Sección 7.2 utilizamos esta aproximación para ayudarnos a determinar aproximadamente las primas, por ejemplo, fijando objetivos de beneficio. Específicamente, en las secciones 7.2.1 y 7.2.2, introducimos los dos métodos predominantes en la práctica para determinar primas, el método de la prima pura y el del ratio de siniestralidad.
Los Siniestros en la ecuación (7.1) son aleatorios y por tanto, como referencia, utilizamos los costes esperados para determinar las tarifas. Existen diferentes maneras de argumentar esta perspectiva que ampliaremos en la Sección 7.3. Por ahora, supondremos que el asegurador suscribe muchos contratos con riesgos similares, excepto que, por pura casualidad, en algunos casos el acontecimiento asegurado ocurre y en otros no. El asegurador se obliga a pagar la cantidad total de reclamaciones por siniestros de todos sus contratos. Si los riesgos son similares, entonces todos los asegurados deberían aportar la misma cantidad, que sería el pago medio por siniestro. Desde esta perspectiva, tiene sentido focalizarnos en el pago medio de los siniestros de un conjunto de asegurados. De la teoría de la probabilidad, específicamente de la ley de los grandes números, sabemos que la media de riesgos iid se aproxima a la cantidad esperada, por lo que podemos utilizar la esperanza matemática como un principio básico de tarificación.
No obstante, utilizando la siniestralidad esperada, esencialmente suponemos que la incertidumbre es inexistente. Si los aseguradores suscriben suficientes pólizas independientes, ésta puede ser una aproximación razonable. Sin embargo, habrá otros casos, como en un contrato único para una gran empresa en el que se aseguran todos sus edificios por incendio, donde el uso exclusivo de una esperanza matemática para tarificar no será suficiente. Por esta razón, en la Sección 7.3, también resumiremos los principios alternativos de tarificación que incorporan la incertidumbre a nuestra fijación de precios. Nótese que un especial énfasis de este texto es la estimación de la distribución entera de la siniestralidad para que el analista no se vea restringido a trabajar sólo con la esperanza matemática.
Los métodos de tarificación conjuntos derivados de la ecuación (7.1) se centran en colecciones de riesgos homogéneos que son similares excepto por la ocurrencia o no de siniestros aleatorios. En el lenguaje estadístico que hemos introducido, esto es una discusión sobre si los riesgos presentan distribuciones idénticas o no. Por supuesto, cuando examinamos los riesgos suscritos por los aseguradores, encontramos muchas variaciones en los riesgos asegurados, incluyendo las características de los contratos y de las personas aseguradas. En la Sección 7.4 extendemos las consideraciones de tarificación para colecciones de riesgos heterogéneos.
En la Sección 7.5 introducimos algunas ideas sobre desarrollo y tendencia. Cuando tarificamos, queremos utilizar la experiencia de siniestralidad más reciente porque el objetivo es definir tarifas con una visión prospectiva. Sin embargo, al inicio de un contrato, la experiencia de siniestralidad reciente es a menudo desconocida; pueden pasar varios años hasta que se produzca completamente. Por esta razón, en esta sección, se introducen los conceptos necesarios para incorporar la experiencia de siniestralidad reciente en el desarrollo de nuestra prima. Desarrollo y tendencia de la experiencia de siniestralidad está relacionada, pero también difiere, de la idea de la tarificación basada en la experiencia que sugiere que la experiencia revela información no disponible a priori sobre el asegurado y que tendría que ser incorporada en consonancia con nuestro punto de vista prospectivo. El Capítulo 9 presenta esta idea con más detalle.
La sección final de este capítulo introduce métodos para seleccionar una prima. Esto será realizado mediante la comparación entre un método de tarificación y la siniestralidad de la cartera analizada y seleccionando el método que produce un mejor ajuste con los datos analizados. Para una cartera de seguros típica, la mayoría de pólizas no declaran siniestros, esto es, no comportan pérdidas. Como la distribución de los siniestros analizados es una combinación de (un número grande de) ceros y cantidades continuas, técnicas especiales serán útiles aquí. La Sección 7.6 introduce los conceptos de curvas de concentración y los correspondientes estadísticos de Gini para ayudar en esta selección.
El capítulo también incluye un suplemento técnico sobre la regulación gubernamental referente a las tarifas del seguro para mantener nuestro trabajo en el marco de las aplicaciones reales.
7.2 Métodos de Tarificación Conjunta
En esta sección, se aprende cómo:
- Definir una prima pura como un coste de siniestralidad, tanto en términos de frecuencia como de severidad
- Calcular una tarifa específica utilizando primas puras, gastos, y márgenes de beneficio
- Definir una ratio de siniestralidad (loss ratio, en inglés)
- Calcular un cambio de tarifa específica utilizando ratios de siniestralidad
- Comparar los métodos de prima pura y de ratio de siniestralidad para determinar primas
Es común considerar la experiencia conjunta de una cartera de seguros. Compatible con la notación anterior, consideramos una colección de n contratos con siniestros \(X_1, \ldots, X_n\). En esta sección, suponemos que los contratos tienen la misma distribución de siniestralidad, en otras palabras forman una cartera homogénea, y, por tanto, son iid. Como justificación, podemos pensar en un seguro personal como el de automóvil o hogar, donde los aseguradores suscriben muchos contratos de riesgos muy similares. En tal caso, la suposición de distribuciones idénticas no es tan limitativa como podríamos pensar en un principio. En la Sección 7.4.1 introduciremos la idea de una exposición variable que nos permitirá rescalar la experiencia de siniestralidad para hacerla comparable. Por ejemplo, rescalando los siniestros seremos capaces de tratar los siniestros de hogar de una casa de 100.000 y los de una casa de 200.000 como pertenecientes a una misma distribución. Por ahora, sencillamente suponemos que \(X_1, \ldots, X_n\) son iid.
7.2.1 Método de la Prima Pura
Si el número en el grupo, n, es grande, entonces la media proporciona una buena aproximación de la siniestralidad esperada
\[ \small{ \mathrm{E}(X) \approx \frac{\sum_{i=1}^n X_i}{n} = \frac{\text{Siniestralidad}}{\text{Exposición}} = \text{Prima Pura}. } \]
Con este enfoque, definimos la prima pura como la suma de los siniestros dividida por la exposición; y que también es conocida como coste de siniestralidad. En el caso de riesgos homogéneos, todas las pólizas son tratadas igual y podemos utilizar el número de pólizas n para la exposición. En la Sección 7.4.1 extendemos el concepto de exposición cuando las pólizas no son iguales.
Podemos multiplicar y dividir por el número de reclamaciones, claim count en inglés, para conseguir
\[ \small{ \text{Prima Pura} = \frac{\text{número de reclamaciones}}{\text{Exposición}} \times \frac{\text{Siniestralidad}}{\text{número de reclamaciones}} = \text{frecuencia} \times \text{severidad} . } \]
Por lo tanto, cuando calculamos las primas utilizando el método de la prima pura, podemos considerar tanto la siniestralidad media (coste de siniestralidad) como la aproximación frecuencia-severidad.
Para conseguir estar más cerca de las aplicaciones prácticas, volvemos ahora a la ecuación (7.1) que también incluye los gastos. La ecuación (7.1) también se refiere al Margen de beneficio para incluir el beneficio de suscripción. Si éste lo relacionamos con las primas, lo denominaremos recargo de beneficio. Como los siniestros son inciertos, el asegurador debe disponer de capital suficiente para asegurar que todas las reclamaciones serán pagadas. Mantener este capital extra es un coste del propio negocio, los inversores de la compañía deben ser compensados por ello, de ahí el recargo extra.
A continuación, descomponemos los Gastos en aquellos que varían según la prima, Variables, y los que no, Fijos de modo que Gastos = Variables + Fijos. Pensando en los gastos variables y los beneficios como una fracción de las primas, definimos
\[ \small{ V = \frac{\text{Variables}}{\text{Prima}} ~~~ \text{y}~~~ Q = \frac{\text{Margen de beneficio}}{\text{Prima}} ~. } \]
Con estas definiciones y la ecuación (7.1), podemos escribir
\[ \small{ \begin{matrix} \begin{array}{ll} \text{Prima} &= \text{Siniestros + Fijos} + \text{Prima} \times \frac{\text{Variables + Margen de beneficio }}{\text{Prima}} \\ & = \text{Siniestros + Fijos} + \text{Prima} \times (V+Q) . \end{array} \end{matrix} } \]
Despejando
\[\begin{equation} \small{ \text{Prima} = \frac{\text{Siniestros + Fijos}}{1-V-Q} . } \tag{7.2} \end{equation}\]
Dividiendo por la exposición, la tarifa puede ser calculada como
\[ \begin{matrix} \begin{array}{ll} \text{Tarifa} &= \frac{\text{Prima}}{\text{Exposición}} = \frac{\text{Siniestros/Exposición + Fijos/Exposición}}{1-V-Q} \\ &= \frac{\text{Prima pura + Fijos/Exposición}}{1-V-Q} ~. \end{array} \end{matrix} \]
En otros términos, esto es
\[ \small{ \text{Tarifa} =\frac{\text{prima pura + gastos fijos por exposición }}{\text{1 – factor de gastos variables – factor de beneficio y contingencias}} . } \]
Ejemplo. CAS Examen 5, 2004, Número 13. Determinar la tarifa de referencia por unidad de exposición, dada la información siguiente:
- Frecuencia por unidad de exposición = 0,25
- Severidad = $100
- Gasto fijo por unidad de exposición = $10
- Factor de gasto variable = 20%
- Factor de beneficio y contingencias = 5%
Solución del Ejemplo
Del ejemplo, nótese que las tarifas calculadas por el método de la prima pura son generalmente denominadas como tarifa de referencia .
De nuestra exposición, nótese también que el beneficio está asociado con aspectos de la suscripción y no con inversiones. Las primas son habitualmente pagadas al principio del contrato por lo que los aseguradores reciben ingresos por la inversión de este dinero. Sin embargo, debido a la naturaleza a corto plazo de estos contratos, los ingresos por la inversión son normalmente ignorados al tarificar. Esto aporta un poco de conservadurismo al proceso, lo que es bien recibido por los aseguradores. Probablemente esto es más relevante en ramos de cola muy larga, como el de accidentes laborales o el de malas prácticas médicas. En estos ramos, a veces pueden pasar 20 años, o incluso más, para resolver las reclamaciones. Pero estos ramos son también los más volátiles; los pagos de siniestros en un futuro lejano son menos extremos cuando se ven desde la perspectiva del descuento financiero.
7.2.2 Método de la Ratio de Siniestralidad
La ratio de siniestralidad (loss ratio, en inglés) es el cociente entre la suma de los siniestros y la prima
\[ \small{ \mathrm{E}(X) \approx \frac{\sum_{i=1}^n X_i}{n} = \frac{\text{Siniestralidad}}{\text{Exposición}} = \text{Prima Pura}. } \]
Cuando calculamos primas, es un poco contra intuitivo focalizarnos en esta ratio porque la componente prima está incorporada en su denominador. Como veremos, la idea es que el método de ratio de siniestralidad proporciona cambios de tarifa más que tarifas en sí; podemos utilizar cambios de tarifa para actualizar la experiencia pasada y así determinar la tarifa actual. Para hacer esto, los cambios de tarifa consisten en la ratio entre la ratio de siniestralidad observada y la ratio de siniestralidad objetivo. Este factor de ajuste es entonces aplicado a las tarifas actuales para conseguir las nuevas tarifas.
Para ver cómo esto funciona en un contexto sencillo, volvemos a la ecuación (7.1) pero ahora ignorando los gastos: \(\small{\text{Prima = Siniestros + Margen Beneficio}}\). Dividiendo por la prima
\[ \small{ \frac{\text{Margen Beneficio}}{\text{Prima}} = 1 - RS = 1 - \frac{\text{Siniestralidad}}{\text{Prima}} . } \]
Supongamos que tenemos un nuevo “objetivo” del recargo de beneficio, \(Q_{objetivo}\). Suponiendo que los siniestros, la exposición, y otros elementos se mantienen igual, entonces para conseguir el nuevo objetivo de beneficio debemos ajustar la prima. Usamos FC como el factor de cambio que está definido según la expresión
\[ \small{ \frac{\text{nuevo Margen Beneficio}}{\text{Prima}} = Q_{objetivo} = 1 - \frac{\text{Siniestralidad}}{FC \times \text{Prima}}. } \]
Despejando para FC, obtenemos
\[ \small{ FC = \frac{\text{Siniestralidad}}{\text{Prima} \times (1-Q_{objetivo})} = \frac{RS}{1-Q_{objetivo}}. } \]
Por ejemplo, si tenemos un ratio de siniestralidad actual = 85% y un objetivo de recargo de beneficio \(\small{Q_{objetivo}=0,20}\), entonces \(\small{FC = 0,85/0,80 = 1,0625}\), lo que significa que aumentamos primas en un 6,25%.
Ahora veamos cómo funciona incluyendo los gastos en la ecuación (7.1). Podemos utilizar el mismo planteamiento que en la Sección 7.2.1 e iniciar con la ecuación (7.2) y despejando por el recargo de beneficio
\[
\small{
Q = 1 - \frac{\text{Siniestralidad+Fijos}}{\text{Prima}} - V .
}
\]
Interpretamos la cantidad Fijos/Prima + V como la “ratio de gastos operacionales.” Y ahora, fijamos un porcentaje de beneficio Q como objetivo y ajustamos las primas según el “factor de cambio” \(FC\)
\[ \small{ Q_{objetivo} = 1 -\frac{\text{Siniestralidad+Fijos}}{\text{Prima}\times FC} - V . } \]
Despejando para \(FC\)
\[\begin{equation} \small{ FC = \frac{\text{Siniestralidad+Fijos}}{\text{Prima} \times (1 - V - Q_{objetivo})}. } \tag{7.3} \end{equation}\]
Ejemplo. Factor de Cambio de Ratio de Siniestralidad. Suponemos la información siguiente:
- Ratio de siniestralidad proyectado = 65%
- Ratio de gastos fijos proyectados = 6,5%
- Gastos variables = 25%
- Margen Beneficio objetivo = 10%
Con estos supuestos y la ecuación (7.3), el factor de cambio puede ser calculado como
\[ \small{ FC = \frac{\text{(Siniestralidad+Fijos)}/\text{Prima}}{1 - V - Q_{objetivo}} = \frac{0,65 + 0,065}{1- 0,25 – 0,10} = 1,10. } \]
Esto significa que el nivel general de la tarifa tendría que ser aumentado en un 10%.
Más adelante, en la Sección 7.5.3, proporcionaremos una comparación entre los métodos de prima pura y ratio de siniestralidad. Como avance, esta sección requerirá los conocimientos sobre exposiciones, tendencias y primas definidos en la Sección 7.5.
7.3 Principios de Tarificación
En esta sección, se aprende cómo:
- Describir los principios actuariales de tarificación más comunes
- Describir las propiedades de los principios de tarificación
- Escoger un principio de tarificación basándose en una propiedad deseada
Existen diferentes aproximaciones para la tarificación según el tipo de contrato. Por ejemplo, el seguro de automóvil para particulares es conocido como una parte importante del mercado minorista de seguros generales en el Reino Unido. En este caso, podemos esperar realizar la tarificación basándonos en un conjunto grande de contratos independientes, una situación en la que las esperanzas matemáticas de los siniestros proporcionan un punto de partida excelente. Por el contrario, un actuario puede tener que tarificar un contrato de seguro para un gran empresario que desea cubrir los complejos beneficios de salud para miles de empleados. En tal caso, el conocimiento de la distribución entera de los siniestros potenciales, no tan solo su valor esperado, es crucial para empezar las negociaciones de la tarifa. Para cubrir una gran gama de potenciales aplicaciones, en esta sección se describen los principales principios de tarificación y sus propiedades, que pueden utilizarse para decidir qué principio en concreto es aplicable en una situación determinada.
7.3.1 Principios de Tarificación
Este capítulo introduce los tradicionales principios de tarificación actuariales basados tan solo en la distribución de la siniestralidad; el precio no depende de la demanda de seguros u otros aspectos de los costes como los gastos. Suponemos que la siniestralidad \(X\) tiene una función de distribución \(F(\cdot)\) y que existen algunas funciones \(H\) que retorna \(F(\cdot)\) en la línea real positiva, denotado como \(P = H(F)\). Para propósitos de notación, es a menudo conveniente sustituir la variable aleatoria \(X\) por su función de distribución y escribir \(P = H(X)\). La tabla 7.1 proporciona varios ejemplos.
| Descripción | Definición (\(H(X)\)) |
|---|---|
| Prima neta (pura) | \(E[X]\) |
| Valor esperado | \((1+\alpha)E[X]\) |
| Desviación estándar | \(E[X]+\alpha SD(X)\) |
| Varianza | \(E[X]+\alpha Var(X)\) |
| Utilidad cero | Solución de \(u(w) = E u(w + P - X)\) |
| Exponencial | \(\frac{1}{\alpha} \ln E e^{\alpha X}\) |
Un principio de tarificación es similar a una medida de riesgo como las introducidas en la Sección 10.3. Matemáticamente, en ambos casos, son funciones que convierten la variable aleatoria (rv) de siniestralidad de interés en un valor numérico. Desde un punto de vista práctico, un principio de tarificación proporciona una guía de qué cantidad cobrará un asegurador para aceptar un riesgo \(X\). En cambio, una medida de riesgo cuantifica el nivel de incertidumbre, o riskiness en inglés, que un asegurador puede utilizar para decidir un nivel de capital suficiente para asegurar su solvencia.
Como se aprecia en la Tabla, la prima neta, o pura, esencialmente supone que no existe incertidumbre. Los principios del valor esperado, la desviación estándar y la varianza añaden un recargo explícito para la incertidumbre a través del parámetro \(\alpha \ge 0\). Para el principio de utilidad cero, pensamos en un asegurador con función de utilidad \(u(\cdot)\) y riqueza w al que le resulta indiferente aceptar o no aceptar el riesgo \(X\). En este caso, \(P\) es conocido como el precio de indiferencia o, en economía, como precio de reserva. Con la utilidad exponencial, el principio de utilidad cero se reduce al principio de tarificación exponencial, esto es, suponiendo \(u(x) = (1-e^{-\alpha x})/\alpha\).
Para valores pequeños de los parámetros de riesgo, el principio de varianza es aproximadamente igual al principio exponencial, como se ilustra en el siguiente caso especial.
Caso especial: Distribución Gamma . Consideramos una siniestralidad distribuida como una gamma con parámetros \(\alpha\) y \(\theta\). Del Apéndice D en 18, la media es \(\alpha \theta\) y la varianza es \(\alpha \theta^2\). Utilizando \(\alpha_{Var}\) como parámetro de riesgo, el principio de varianza es \(H_{Var}(X) = \alpha \theta+\alpha_{Var} (\alpha \theta^2)\). Del mismo apéndice, es directo derivar la función generadora de momentos, \(M(t) = E e^{tX} = (1-t\theta)^{-\alpha}\). Con esto y un parámetro de riesgo \(\alpha_{Exp}\), podemos expresar el principio exponencial como
\[ H_{Exp}(X) = \frac{-\alpha}{\alpha_{Exp}} \ln\left(1-\alpha_{Exp} \theta\right). \]
Para ver la relación entre \(H_{Var}(X)\) y \(H_{Exp}(X)\), escogemos \(\alpha_{Exp} = 2 \alpha_{Var}\). Con una aproximación de cálculo (\(\ln(1-x) = -x - x^2/2 - x^3/3 - \cdots\)), podemos escribir
\[ H_{Exp}(X) = \frac{-\alpha}{\alpha_{Exp}} \ln\left(1-\alpha_{Exp} \theta\right) = \frac{-\alpha}{\alpha_{Exp}} \left\{ -\alpha_{Exp} \theta -(\alpha_{Exp} \theta)^2/2 - \cdots\right\} \\ \approx \alpha \theta + \frac{\alpha_{Exp}}{2}(\alpha \theta^2 ) = H_{Var}(X). \]
7.3.2 Propiedades de los Principios de Tarificación
Las propiedades de los principios de tarificación nos ayudan como guía en la selección de un principio de tarificación en las aplicaciones prácticas. La Tabla 7.2 proporciona algunos ejemplos de las propiedades de estos principios.
| Descripción | Definición |
|---|---|
| Recargo no negativo | \(H(X) \ge E[X]\) |
| Aditividad | \(H(X_1+X_2) = H(X_1) + H(X_2)\), para \(X_1, X_2\) independientes |
| Invariancia de escala | \(H(cX) = c H(X)\), para \(c \ge 0\) |
| Consistencia | \(H(c+X) = c + H(X)\) |
| Acotabilidad | \(H(X) \le max ~range ~\{X\}\) |
Esta tabla es sencillamente un subconjunto de las muchas propiedades citadas en la literatura actuarial. Por ejemplo, el artículo de Young (2014) lista 15 propiedades. Véase también las propiedades descritas como axiomas coherentes que introducimos para las medidas de riesgo en la Sección 10.3.
Algunas de las propiedades listadas en la Tabla 7.2 son suaves en el sentido que casi siempre serán satisfechas. Por ejemplo, la propiedad de acotabilidad indica que el recargo de la prima será más pequeño que el valor máximo de la siniestralidad \(X\). Otras propiedades pueden no ser tan suaves. Por ejemplo, para una cartera de riesgos independientes, el actuario puede querer que se cumpla la propiedad de aditividad. Es fácil ver que esta propiedad se cumple para los principios del valor esperado, varianza, y exponencial, pero no para el principio de desviación estándar. Otro ejemplo es la propiedad de consistencia que no se cumple para el principio de valor esperado cuándo el parámetro de riesgo del recargo \(\alpha\) es positivo.
El principio de invariancia de escala es conocido como homogeneidad de grado uno en economía. Nos permite, por ejemplo, trabajar con monedas diferentes (p. ej., de dólares a Euros), así como en otras aplicaciones que serán comentadas más adelante en la Sección siguiente 7.4. A pesar de que es un principio generalmente aceptado, nótese que este principio no se cumple para unos valores grandes de \(X\) que pueden limitar los beneficios de un asegurador; si un asegurador tiene una probabilidad elevada de devenir insolvente, entonces el asegurador no deseará utilizar un criterio lineal de tarificación. Es fácil comprobar que este principio se cumple para los principios del valor esperado y desviación estándar, pero no para los principios de varianza y exponencial.
7.4 Riesgos Heterogéneos
En esta sección, se aprende cómo:
- Describir exposiciones de seguro en términos de escala de distribuciones
- Explicar una exposición en términos de algunos tipos de seguro comunes, como los seguros de automóvil y hogar
- Describir cómo los factores de tarificación pueden utilizarse para tener en cuenta la heterogeneidad entre los riesgos de una cartera
- Medir el impacto de los factores de tarificación mediante relatividades
Como se apuntó en la Sección 7.1, hay mucha variabilidad en los riesgos que son asegurados, las características de los contratos, y en las personas aseguradas. Como ejemplo, podríamos tener un hermano o hermana gemelo que trabaja en la misma ciudad y gana una cantidad similar de dinero. Aún así, cuando llegara el momento de seleccionar opciones en el seguro de alquiler que cubriera los contenidos de nuestros apartamentos, nos podemos imaginar que existirían diferencias en la cantidad de contenidos asegurables, en las elecciones de las franquicias para definir la cantidad retenida, y quizás niveles diferentes de incertidumbre según la seguridad relativa de nuestros barrios. Las personas y los riesgos que se aseguran son diferentes.
Cuando pensamos en una colección de riesgos diferentes, o heterogéneos, una opción puede ser tarificar todos los riesgos igual. Esta opción es común, por ejemplo, cuando el gobierno patrocina programas para el riesgo de inundación o el seguro de salud. Sin embargo, también es común tener precios diferentes, con diferencias que guarden relación con el riesgo asegurado.
7.4.1 Exposición al Riesgo
Una manera directa para hacer que los riesgos heterogéneos sean comparables es a través del concepto exposición. Para explicar el concepto, podemos usar las distribuciones de escala que aprendimos en el Capítulo 3. Como recordatorio, una distribución de escala, supone que \(X\) sigue una distribución paramétrica y que definimos una versión reescalada con \(R = X/E\), \(E > 0\). Si \(R\) pertenece a la misma familia paramétrica que \(X\), entonces la distribución se denomina como distribución de escala. Como ya vimos, las distribuciones gamma, exponencial y Pareto son ejemplos de distribuciones de escala.
Intuitivamente, la idea detrás de las exposiciones es conseguir que los riesgos sean más comparables uno con otro. Por ejemplo, puede ser que los riesgos \(X_1, \ldots, X_n\) sigan distribuciones diferentes y aun así, con la elección de unas exposiciones correctas, los cocientes \(R_1, \ldots, R_n\) sigan una misma distribución. Aquí, interpretaremos los cocientes \(R_i = X_i/E_i\) como la siniestralidad dividida por la exposición.
Tabla 7.3 proporciona unos cuantos ejemplos. Remarcamos que esta tabla se refiere a años “imputados” de automóviles y a años de hogar, conceptos que serán explicados en la Sección 7.5.
\[ \small{ \begin{matrix} \begin{array}{ll} \text{Tipo de Seguro} & \text{Exposición Base} \\\hline \text{Automóvil Particular} & \text{Año Imputado Automóvil, Importe de la Cobertura de Seguro } \\ \text{Hogar} & \text{Año Imputado Hogar, Importe de la Cobertura de Seguro}\\ \text{Accidentes de Trabajo} & \text{Salario}\\ \text{Responsabilidad Civil Comercial} & \text{Facturación, Salario, Superficie cuadrada, Número de Unidades}\\ \text{Daños Empresariales} & \text{Importe de la Cobertura de Seguro}\\ \text{Responsabilidad Civil Profesional del Médico} & \text{Número de Años de Experiencia }\\ \text{ Responsabilidad Civil Profesional} & \text{Número de Profesionales (p.ej., Abogados o Contables)}\\ \text{Objetos Personales} & \text{Valor del Ítem} \\ \hline \end{array} \end{matrix} } \]
Tabla 7.3 : Exposiciones Comúnmente Utilizadas para Diferentes Tipos de Seguro
Una exposición es un tipo de factor de tarificación, concepto que definiremos explícitamente en la próxima Sección 7.4.2. Es probablemente el factor más importante, tan importante que tanto las primas como los siniestros están definidos en términos de “por exposición”.
Para modelizar la frecuencia y la severidad, es habitual pensar en la frecuencia como proporcional a la exposición y en la severidad en términos de pérdida por reclamación (no dependiente de la exposición). Con todo, no siempre es así. Para muchos ramos, es conveniente usar exposiciones proporcionales a la inflación. La inflación no se relaciona habitualmente con la frecuencia, pero es proporcional a la severidad.
Criterios para Escoger una Exposición
Una base o medida de la exposición debería atender a los criterios siguientes:
- ser una medida precisa de la exposición cuantitativa a la pérdida,
- ser fácilmente determinada por el asegurador (cuando la póliza se calcula) y que no esté sujeta a manipulación por parte del asegurado,
- ser fácil de entender para el asegurado y fácil de calcular para el asegurador,
- que considere cualquier base de exposición preexistente establecida dentro de la industria, y
- para algunos ramos, que sea proporcional a la inflación. De este modo, las tarifas no son sensibles al cambio de valor del dinero con el tiempo, al estar incluido en la base de exposición.
Como ilustración, consideremos la cobertura particular de automóvil. En lugar de utilizar la base de exposición “año imputado automóvil,” una medida más precisa de la exposición cuantitativa a la pérdida podría ser el número de millas conducidas. Sin embargo, esta medida es difícil de determinar cuando se emite la póliza y está sujeta a una potencial manipulación por parte del asegurado.
En otro ejemplo, la medida de exposición en los daños empresariales, p. ej. seguro de incendio, es a menudo la cantidad de cobertura del seguro. Como el valor de los objetos crecen con la inflación, el importe de la cobertura del seguro también aumentará. Así, las tarifas definidas a partir del importe de la cobertura del seguro son menos sensibles a la inflación que si lo fueran de otro modo.
7.4.2 Factores de Tarificación
Un factor de tarificación, o variable de tarificación, es sencillamente una característica del asegurado o del riesgo asegurado por la que la tarifa cambia. Por ejemplo, cuando se adquiere un seguro de automóvil, es probable que el asegurador tenga tarifas distintas por edad, género, tipo de automóvil y donde se guarda, historial de accidentes, y otras variables. Estas variables son conocidas como factores de tarificación. A pesar de que algunas variables pueden ser continuas, como la edad, la mayoría son categóricas - factor es una etiqueta utilizada para variables categóricas. De hecho, incluso para variables continuas como la edad, es común categorizarlas para crear grupos como “jóvenes,” “adultos,” y “mayores” utilizados al tarificar.
Tabla 7.4 proporciona algunos ejemplos. En muchos países, el mercado de seguro de particulares (p. ej., automóvil y hogar) es muy competitivo, por lo que utilizar 10 o 20 variables para tarificar es habitual.
\[ \small{ \begin{matrix} \begin{array}{l|l}\hline \text{Tipo de Seguro} & \text{Factores De Tarificación}\\\hline\hline \text{Automóvil Particulares } & \text{Edad y Género del Conductor, Año del Modelo, Historial de Accidentes}\\ \text{Hogar} & \text{Importe del Seguro, Antigüedad del Hogar, Tipo de Construcción}\\ \text{Accidentes de Trabajo} & \text{Clase Ocupacional}\\ \text{Responsabilidad Civil Empresarial} & \text{Sector, Territorio, Límite de Responsabilidad}\\ \text{Responsabilidad Civil Médica} & \text{Especialidad, Territorio, Límite de Responsabilidad}\\ \text{Automóvil Empresas} & \text{Tipo de Conducción, Territorio, Límite de Responsabilidad}\\ \hline \end{array} \end{matrix} } \] Tabla 7.4 : Factores de Clasificación Comúnmente Utilizados en Diferentes Tipos de Seguro
Ejemplo. Siniestros y Prima por Importe del Seguro y Territorio. Como ilustración, Tabla 7.5 presenta unos sencillos datos ficticios tomados de Werner and Modlin (2016). Los datos constan de los siniestros y los gastos asociados de pérdida (LossLAE por sus siglas en inglés), segmentados por tres niveles de importe del seguro (AOI por sus siglas en inglés), y por tres territorios (Terr). Para cada combinación de AOI y Terr, también tenemos disponibles el número de pólizas emitidas, que actúa como Exposición.
\[ \small{ \begin{matrix} \begin{array}{cc|rrr} \hline AOI & Terr & Exposición & LossLAE & Prima \\\hline \text{Bajo} & 1 & 7 & 210,93 & 335,99 \\ \text{Medio} & 1 & 108 & 4.458,05 & 6.479,87 \\ \text{Alto} & 1 & 179 & 10.565,98 & 14.498,71 \\\hline \text{Bajo} & 2 & 130 & 6.206,12 & 10.399,79 \\ \text{Medio} & 2 & 126 & 8.239,95 & 12.599,75 \\ \text{Alto} & 2 & 129 & 12.063,68 & 17.414,65 \\\hline \text{Bajo} & 3 & 143 & 8.441,25 & 14.871,70 \\ \text{Medio} & 3 & 126 & 10.188,70 & 16.379,68 \\ \text{Alto} & 3 & 40 & 4.625,34 & 7.019,86 \\ \hline \text{Total} & & 988 & 65.000,00 & 99.664,01 \\\hline \hline \end{array} \end{matrix} } \] Tabla 7.5 : Siniestros y Prima por Importe del Seguro y Territorio
En este ejemplo, los factores de tarificación AOI y Terr producen nueve celdas. Nótese que se podría combinar la celda “territorio 1 con un nivel bajo de importe de seguro” con otra celda porque sólo hay 7 pólizas en dicha celda. Este cambio sería perfectamente aceptable - consideraciones de este tipo son unas de las principales tareas del analista. Una introducción sobre la selección de variables se encuentra en el Capítulo 8, incluyendo el Suplemento Técnico TS 8.B. Alternativamente, también se podría pensar en reforzar la información sobre la celda (Terr 1, AOI Bajo) “tomando prestada” información de las celdas vecinas (p. ej., otros territorios con el mismo AOI, u otras cantidades de AOI dentro del Terr 1). Este enfoque es el tema de credibilidad que será desarrollado en el Capítulo ??.
Para entender el impacto de los factores de tarificación, es habitual el uso de relatividades. Una relatividad es la diferencia del riesgo esperado entre un nivel concreto de un factor de tarificación y un valor aceptado como referencia. En este libro, trabajamos con relatividades definidas a través de ratios; aunque también es posible definirlas mediante diferencias aritméticas. Por tanto, nuestras relatividades están definida como
\[ \text{Relatividad}_j = \frac{\text{(Siniestralidad/Exposición)}_j}{\text{( Siniestralidad/Exposición)}_{Base}} . \]
Ejemplo. Siniestros y Prima por Importe del Seguro y Territorio - Continuación. Los métodos tradicionales de clasificación sólo consideran una variable de clasificación a la vez - son univariantes. Por tanto, si quisiéramos relatividades de los siniestros y gastos (LossLAE) por importe del seguro, podríamos sumar territorios para conseguir la información mostrada en Tabla 7.6.
\[ \small{ \begin{matrix} \begin{array}{c|rrrr} \hline AOI & Exposición & LossLAE & LossLAE/Exp &Relatividad \\\hline \text{Bajo} & 280 & 14858,3 & 53,065 &0,835 \\ \text{Medio} & 360 & 22886,7 & 63,574 &1,000 \\ \text{Alto} & 348 & 27255,0 & 78,319 & 1,232 \\\hline \text{Total} & 988 & 65.000,0 & \\\hline \hline \end{array} \end{matrix} } \]
Tabla 7.6 : Siniestros y Relatividades por Importe del Seguro
Así, por ejemplo, los siniestros y gastos por unidad de exposición son un 23,2% más altos para los riesgos con un importe del seguro alto comparado con aquellos con un importe medio. Estas relatividades no distinguen por territorio.
La introducción de factores de calificación permite al analista crear celdas que definen pequeñas colecciones de riesgos; el objetivo es elegir la combinación correcta de factores de calificación para que todos los riesgos de una celda puedan ser tratados de la misma manera. En la terminología estadística, queremos que todos los riesgos de una celda tengan la misma distribución (sujeta a un cambio de escala por una variable de exposición). Esta es la base de la tarificación de los seguros. Todos los riesgos de una casilla tienen el mismo precio, pero los riesgos de distintas casillas pueden tener precios diferentes.
Dicho de otro modo, los aseguradores pueden cobrar diferentes tarifas para riesgos diferentes; la discriminación de los riesgos es legal y comúnmente realizada. Sin embargo, la base de la discriminación, la elección de los factores de riesgo, es un tema de extenso debate. La comunidad actuarial, los administradores del seguro, los reguladores, y las organizaciones de consumidores son todos participantes activos en este debate. El Suplemento Técnico TS 7.A describe estos asuntos desde una perspectiva reguladora.
A parte de criterios estadísticos para evaluar la importancia de un factor de tarificación, los analistas ponen mucha atención a las preocupaciones empresariales de la compañía (p. ej., ¿es caro implementar un factor de tarificación?), a criterios sociales (¿es una variable bajo el control del asegurado?), a criterios legales (¿existen regulaciones que prohíben el uso de un factor de tarificación como el género?), y a otros asuntos sociales. Estas cuestiones están, en gran parte, fuera del alcance de este texto. Con todo, al ser parte fundamental de la tarificación del seguro, daremos una breve visión general en el Capítulo 8, incluyendo el Suplemento Técnico TS 8.B.
7.5 Desarrollo y Tendencia
En esta sección, se aprende cómo:
- Definir y calcular los diferentes tipos de medida resumen de la exposición y la prima que aparecen en los informes financieros
- Describir el desarrollo de una reclamación sobre varios pagos y enlazarlo con las medidas de los siniestros pendientes, incluyendo aquellos siniestros pendientes de declaración (IBNR por sus siglas en inglés, incurred but not reported) así como los siniestros pendientes de liquidación y pago
- Comparar y contrastar las fortalezas y debilidades relativas de los métodos de tarificación de prima pura y de ratio de siniestralidad
Como vimos en la Sección 7.2, los aseguradores consideran información agregada para la tarificación tal como las exposiciones al riesgo, las primas, los gastos, las reclamaciones, y los pagos. Esta información agregada también es útil para gestionar otras actividades de los aseguradores; por ejemplo, los informes financieros deben ser generalmente reportados al menos anualmente y a menudo trimestralmente. En cualquier momento de realización de dichos informes, la información sobre reclamaciones y pólizas estará en proceso y necesariamente incompleta; esta sección introduce conceptos para proyectar la información del riesgo de modo que sea útil para propósitos de tarificación. La información sobre los riesgos (exposiciones, primas, cuentas de reclamaciones, siniestros, y factores de tarificación) se encuentra habitualmente estructurada en tres bases de datos:
- Base de datos de pólizas - contiene la información sobre el riesgo asegurado, el tomador/asegurado, y las disposiciones contractuales.
- Base de datos de reclamaciones - contiene información sobre cada reclamación; estos datos están enlazados con la base de datos de pólizas.
- Base de datos de pagos - contiene información sobre cualquier transacción de cada reclamación, normalmente pagos pero también cambios en las provisiones por siniestros pendientes. Estos datos están enlazados con la base de datos de reclamaciones.
Con este nivel de detalle de las bases de datos, es sencillo (en principio) resumir a nivel de póliza para agregar la información requerida por los informes financieros. Esta sección describe varias medidas de resumen generalmente utilizadas.
7.5.1 Exposiciones y Primas
Un periodo de reporte financiero es una longitud de tiempo fijada en el calendario; utilizaremos el periodo del 1 de enero hasta el 31 de diciembre para los ejemplos de este libro, aunque otros periodos puedan ser usados habitualmente. El periodo de reporte es fijo pero las pólizas pueden empezar en cualquier momento del año. Incluso si todas las pólizas tuvieran la misma longitud de contrato de (pongamos) un año, debido a los diferentes tiempos de inicio, pueden acabar en cualquier momento de tiempo del periodo de reporte financiero. La Figura 7.1 presenta cuatro pólizas ilustrativas. Debido a los diferentes momentos de inicio y fin, son necesarios algunos estándares sobre qué tipos de medidas son más útiles para resumir la experiencia en un determinado periodo de reporte.
7.1 Cronograma de Exposiciones para Cuatro Pólizas de 12 Meses.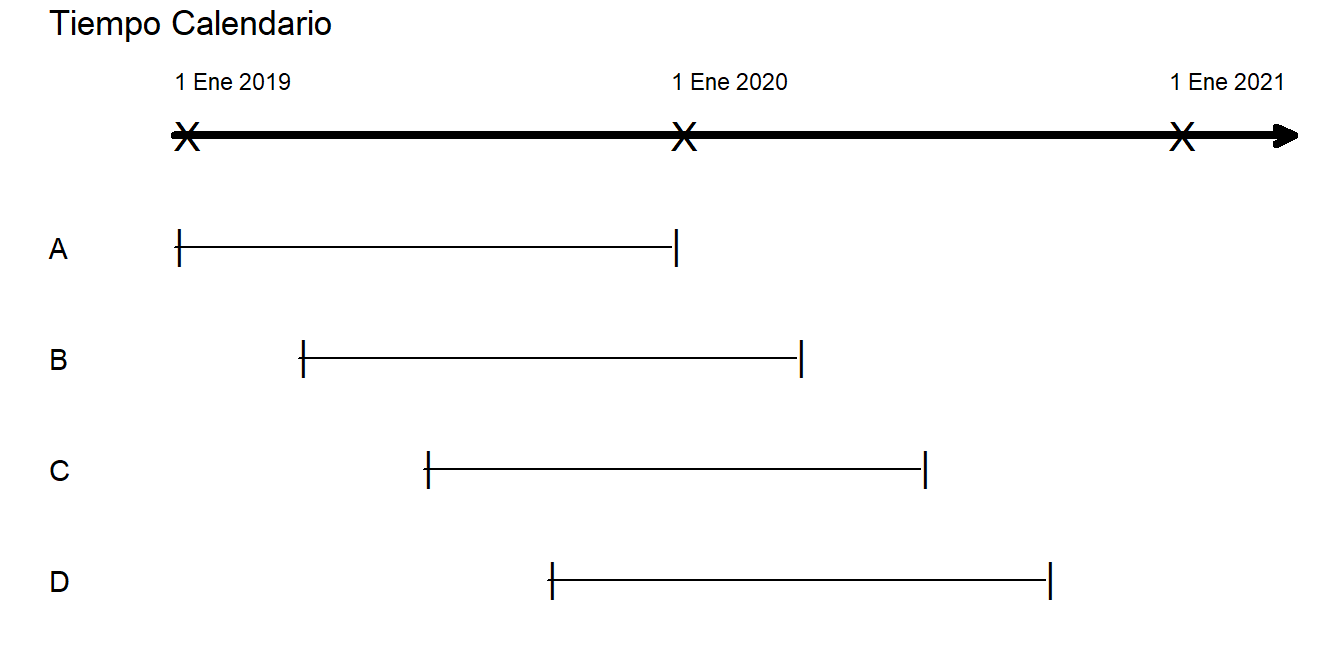
Figure 7.1: (ref:Exposures)
Algunas medidas de exposición utilizadas comúnmente son:
- exposiciones emitidas, la cantidad de exposición en las pólizas emitidas (devengadas y no devengadas) durante el periodo en cuestión,
- exposiciones devengadas, las unidades de exposición efectivamente expuestas a la pérdida durante el periodo, esto es, la cobertura que ya ha sido proporcionada,
- exposiciones no devengadas, representan la porción de las exposiciones emitidas para las que todavía no se ha proporcionado cobertura en este periodo de tiempo, y
- exposiciones en vigor, unidades de exposición expuestas a pérdida en un momento determinado.
La Tabla 7.12 muestra cálculos ilustrativos detallados para las cuatro pólizas.
\[ \small{ \begin{matrix} \begin{array}{cl|cc|cc|cc|c} \hline & & & & & & &&\text{En Vigor} \\ &\text{Efectivo} & \text{Emitida}& \text{Exposición} & \text{Devengada} &\text{Exposición}& \text{No Devengada} &\text{Exposición}& \text{Exposición} \\ {Póliza} &\text{Fecha} & 2019 & 2020 & 2019 & 2020 & 2019 & 2020 & \text{1 Enero 2020} \\ \hline \text{A}&\text{1 Enero 2019} & 1,00 & 0,00 & 1,00 & 0,00& 0,00 & 0,00 & 0,00 \\ \text{B}&\text{1 Abril 2019} & 1,00 & 0,00 & 0,75 & 0,25 & 0,25 & 0,00& 1,00 \\ \text{C}&\text{1 Julio 2019} & 1,00 & 0,00 & 0,50 & 0,50 & 0,50 & 0,00& 1,00 \\ \text{D}&\text{1 Octub 2019} & 1,00 & 0,00 & 0,25 & 0,75 & 0,75 & 0,00& 1,00 \\ \hline & Total & 4,00 & 0,00 & 2,50 & 1,50 & 1,50 & 0,00 & 3,00 \\ \hline \hline \end{array} \end{matrix} } \] Tabla 7.12: Exposiciones para Cuatro Pólizas de 12 Meses
Esta medida de resumen se suele denominar método del año de calendario, en contraste al denominado método del año de póliza. En el último método, todas las pólizas empiezan a principios de año. Este método es útil para los métodos de tarificación basados en contratos individuales que nosotros no trataremos aquí.
Del mismo modo que para las exposiciones, podemos resumir (o agregar) primas. Las primas, igualmente, pueden ser también emitidas, devengadas, no devengadas, o en vigor. Considerar el ejemplo siguiente.
Ejemplo. 7.5.1. CAS Examen 5, 2003, Número 10. Una póliza de 12 meses ha sido emitida el 1 de marzo de 2002 con una prima de 900$. El 31 de diciembre de 2002, ¿cuál de los siguientes casos es cierto?
\[ \small{ \begin{matrix} \begin{array}{l|ccc} \hline & \text{Año Calendario} & \text{Año Calendario} \\ & \text{2002 Emitida} & \text{2002 Devengada} & \text{En vigor} \\ & \text{Prima} & \text{Prima} & \text{Prima} \\\hline A. & 900 & 900 & 900 \\ B. & 750 & 750 & 900 \\ C. & 900 & 750 & 750 \\ D. & 750 & 750 & 750 \\ E. & 900 & 750 & 900 \\\hline \end{array} \end{matrix} } \]
Solución del Ejemplo
7.5.2 Siniestros, Reclamaciones y Pagos
En términos generales, los términos siniestro y reclamación se refieren a la cantidad de la compensación pagada o potencialmente pagable al reclamante bajo los términos previstos en la póliza de seguro. Las definiciones pueden variar:
- A veces, el término reclamación se utiliza indistintamente con el término siniestro.
- En algún seguro y en fuentes actuariales, el término siniestro es utilizado como la cantidad del daño ocasionado en un evento asegurado. La reclamación es la cantidad pagada por el asegurador, con alguna diferencia debido a las franquicias, límites de la póliza, y similares.
- En usos económicos, una reclamación es una demanda de pago hecha por un asegurado o por una víctima que actúa como tercero bajo los términos y condiciones de un contrato de seguro y el siniestro es la cantidad pagada por el asegurador.
En este texto seguiremos el segundo punto. Con todo, al leer otras referencias, deberemos estar alerta sobre las definiciones utilizadas para los términos siniestro y reclamación.
Para establecer más terminología, es útil seguir el cronograma de una reclamación tal y como se desarrolla. En la Figura 7.2, el evento de la reclamación ocurre en el momento \(t_1\) y se notifica a la compañía aseguradora en el momento \(t_3\). Puede haber un largo intervalo de tiempo entre la ocurrencia y la notificación, tal que dicho intervalo de tiempo incluya el momento de cierre del periodo de reporte financiero (\(t_2\)), conocido como fecha de evaluación. En este caso, la reclamación se denomina como pendiente de declaración en esta fecha de evaluación.
Después de ser notificada, puede haber uno o más pagos de siniestro. No siempre todos los pagos pueden ser realizados antes de la próxima fecha de evaluación (\(t_4\)).
A medida que la reclamación se desarrolla, finalmente, la compañía considera sus obligaciones financieras para que la reclamación sea resuelta y declara la reclamación como cerrada. Aun así, es posible que nuevos hechos ocurran y que la reclamación deba ser reabierta, dando lugar a pagos de siniestro adicionales antes de ser cerrada otra vez.
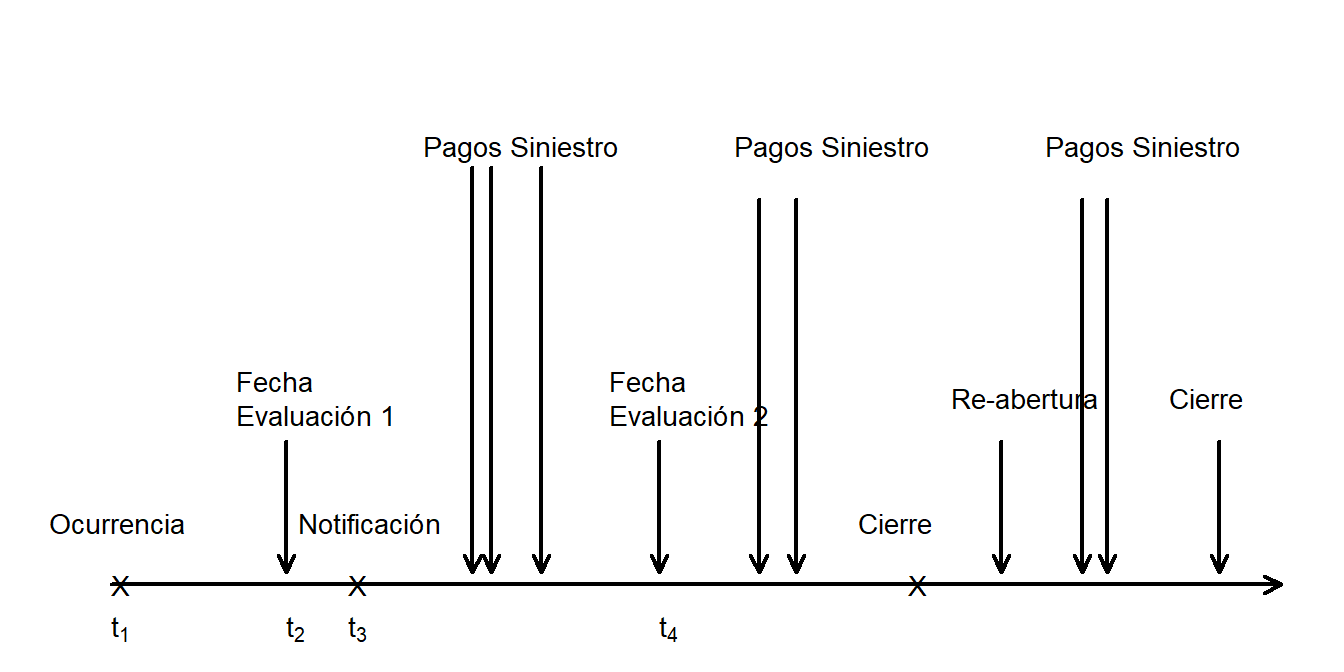
Figure 7.2: Cronograma del Desarrollo de una Reclamación.
- Fecha de Accidente - la fecha de ocurrencia que dio origen a la reclamación. También conocida como fecha de siniestro o fecha de ocurrencia.
- Fecha de Declaración - la fecha en la que el asegurador recibe la notificación de la reclamación. Los siniestros (o reclamaciones) no conocidos actualmente por el asegurador se conocen como siniestros pendientes de declaración o incurred but not reported (IBNR) claims, en inglés.
Hasta que la reclamación está resuelta o liquidada, la reclamación declarada se considera como una reclamación abierta. Una vez la reclamación está resuelta, se clasifica como reclamación cerrada. En algunos casos, puede ocurrir algo más después que la reclamación esté cerrada, y la reclamación puede ser reabierta.
Recordemos que un siniestro es la cantidad pagada o pagable a un reclamante bajo los términos previstos en una póliza de seguro. Además, tenemos
- Siniestros pagados son aquellos siniestros de un periodo determinado que ya han sido pagados a los reclamantes.
- Cuando hay una previsión de que un pago deberá ser hecho en el futuro, la reclamación tendrá una reserva por siniestros pendientes de liquidación y pago, case reserve en inglés, que representa la cantidad estimada de ese pago.
- Siniestros declarados, también conocidos en inglés por case incurred, son Siniestros pagados + Reserva de siniestros pendientes de liquidación y pago.
La siniestralidad definitiva es la cantidad de dinero necesaria para cerrar y resolver todas las reclamaciones para un grupo determinado de pólizas.
7.5.3 Comparación de los Métodos de Prima Pura y Ratio de Siniestralidad
Una vez que hemos aprendido como las exposiciones, las primas, y las reclamaciones se desarrollan en el tiempo, podemos considerar cómo pueden ser utilizadas para la tarificación. Hemos visto que los aseguradores ofrecen muchos tipos diferentes de pólizas que dan cobertura a diferentes asegurados con diferentes cantidades de riesgos. Esta agregación se denomina a veces como mezcla de negocio. Es importante hacer notar que a lo largo del tiempo pueden existir cambios en esta mezcla ya que los asegurados van y vienen, las cantidades de los riesgos varían, etcétera. Las exposiciones, las primas, y los tipos de riesgos de un informe financiero previo pueden no ser representativos del periodo para el que se calculen las tarifas. El proceso de extrapolar exposiciones, primas, y tipos de riesgo es conocido como de tendencia. Por ejemplo, una prima devengada nivelada es aquella prima devengada que resultaría de considerar para todo el periodo las tarifas aplicadas según el periodo efectivo de experiencia. La mayoría de métodos de tendencia son matemáticamente sencillos en la práctica, aunque pueden complicarse por circunstancias contractuales y administrativas. Para más detalle, dirigimos al lector a las referencias estándares tales como Werner and Modlin (2016) y Friedland (2013).
Método de Ratio de Siniestralidad
La expresión para el factor de cambio de tarifa del método de ratio de siniestralidad en la ecuación (7.3) supone una determinada consistencia en la experiencia de la cartera a lo largo del tiempo. Para otro enfoque, podemos definir la ratio de siniestralidad histórica como:
\[ \small{ RS_{histórica} = \frac{\text{siniestros históricos}}{\text{exposición devengada del periodo histórico }\times \text{tarifa actual}}. } \]
Aquí, podemos pensar en la exposición devengada del periodo histórico \(\times\) tarifa actual como la prima histórica.
Utilizando la ecuación (7.2), podemos escribir una ratio de siniestralidad como \[ \small{ RS = \frac{\text{Siniestros}}{\text{Primas}}=\frac{1-V-Q}{\text{(Siniestros + Fijos)}/\text{Siniestros}}=\frac{1-V-Q}{1+G} ~, } \]
donde \(G = \text{Fijos} / \text{Siniestros}\), es la ratio de gastos fijos sobre siniestros. Con esta expresión, definimos la ratio de siniestralidad objetivo
\[ \small{ RS_{objetivo} = \frac{1-V-Q}{1+G} = \frac{1-\text{factor de gastos variables – factor de beneficio y contingencias}} {1+\text{ratio de gastos fijos sobre siniestros}} . } \]
Con esto, el factor de cambio de tarifa es
\[\begin{equation} \small{ FC =\frac{RS_{histórica}}{RS_{objetivo}}. } \tag{7.4} \end{equation}\]
Comparando la ecuación (7.3) con (7.4), podemos ver que la última ofrece más flexibilidad para incorporar explícitamente tendencias históricas. Como el método de ratio de siniestralidad está basado en cambios de proporciones, esta flexibilidad está ciertamente garantizada.
Comparación de Métodos
Suponiendo que exposiciones, primas y reclamaciones han sido tratadas para ser representativas del periodo para el que las tarifas están siendo calculadas, estamos preparados para comparar los métodos de tarificación de prima pura y ratio de siniestralidad. Empezaremos haciendo notar que con los mismos datos de entrada, estas dos aproximaciones producen los mismos resultados. Esto es, son algebraicamente equivalentes. Sin embargo, se basan en diferentes enfoques:
\[ \small{ \begin{array}{l|l}\hline \text{Método Prima Pura} & \text{Método Ratio Siniestralidad} \\ \hline \text{Basado en exposiciones} & \text{Basado en primas} \\ \text{No requiere tarifas existentes} & \text{Requiere tarifas existentes} \\ \text{No utiliza primas niveladas} & \text{Utiliza primas niveladas} \\ \text{Produce tarifas} & \text{Produce cambios de tarifas} \\ \hline \end{array} } \]
Comparando los métodos de tarificación de prima pura y ratio de siniestralidad, podemos ver que:
- El método de prima pura requiere una exposiciones bien definidas y sensibles al cambio.
- El método de ratio de siniestralidad no puede ser utilizado para un nuevo ramo porque produce cambios de la tarifa actual.
- El método de prima pura es preferible cuando puede ser difícil calcular la prima nivelada. En algunos casos, como los ramos de negocios donde los ajustes de la tarifa del riesgo individual se hacen a pólizas individuales, es difícil determinar la prima devengada nivelada necesaria para utilizar el método de ratio de siniestralidad.
En muchos países desarrollados como los EE.UU. donde la mayoría de ramos existen desde hace décadas, el método de ratio de siniestralidad es el más popular.
Ejemplo. 7.5.2. CAS Examen 5, 2006, Número 36. Sea la información siguiente :
- Primas devengadas niveladas para el periodo de experiencia = 500.000$
- Siniestros con tendencia según periodo de experiencia = 300.000$
- Exposición devengada del periodo de experiencia = 10.000
- Factor de gastos variables = 23%
- Gastos fijos = 21.000$
- Factor de beneficios y contingencias = 5%
- Calcula el cambio de nivel de tarifa utilizando el método de ratio de siniestralidad.
- Calcula el cambio de nivel de tarifa utilizando el método de prima pura.
- Describe una situación en la que es preferible utilizar el método de ratio de siniestralidad, y una situación en la que es preferible utilizar el método de prima pura.
Mostrar solución del ejemplo
7.6 Selección de Prima
En esta sección, se aprende cómo:
- Describir distribuciones no simétricas mediante una curva de Lorenz y un índice de Gini
- Definir una curva de rendimiento y el correspondiente estadístico de Gini
- Utilizar la curva de rendimiento y el estadístico de Gini para seleccionar la prima mediante validación cruzada
En una cartera de contratos de seguro, los aseguradores reciben primas y pagan siniestros. Después de realizar sendos ajustes para los gastos y las consideraciones sobre beneficio, podrían resultar útiles herramientas para comparar las distribuciones de primas y siniestros a la hora de seleccionar un principio de cálculo de la prima.
7.6.1 Curva de Lorenz Clásica
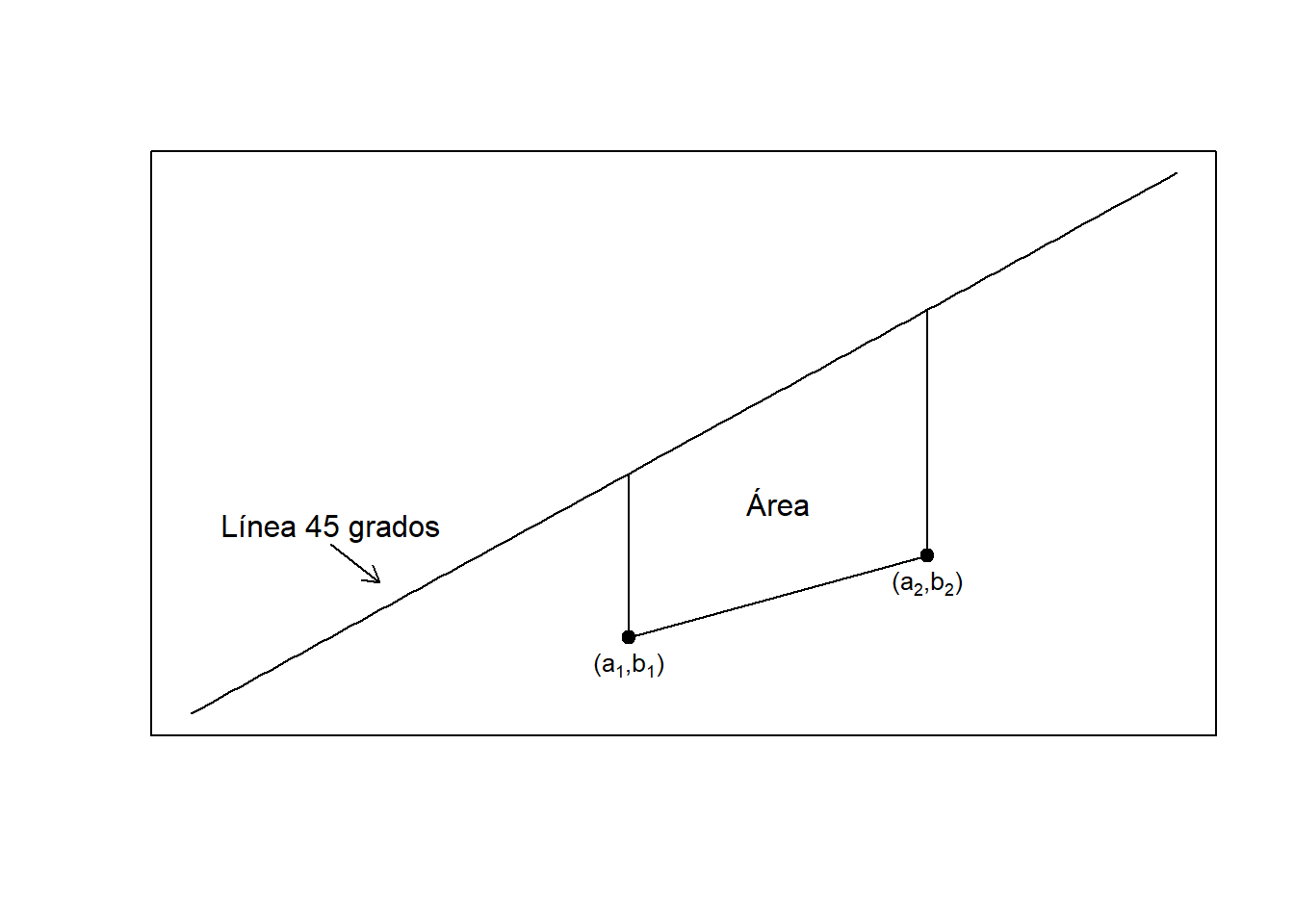
En economía del bienestar, es común comparar distribuciones vía la curva de Lorenz, desarrollada por Max Otto Lorenz (Lorenz 1905). Una curva de Lorenz es un gráfico de la proporción de una población en el eje horizontal y una función de distribución de interés en el eje vertical. Normalmente se utiliza para representar distribuciones de ingresos. Cuando la distribución de ingresos está perfectamente alineada con la distribución de población, la curva de Lorenz resultante es una recta de 45 grados denominada como línea de igualdad. Como el gráfico compara dos funciones de distribución, podemos pensar en la curva de Lorenz como un tipo de pp plot que fue introducido en la Sección 4.1.2.1. El área entre la curva de Lorenz y la línea de igualdad es una medida de la discrepancia entre las distribuciones de ingresos y población. Dos veces esta área nos proporciona el conocido índice de Gini, introducido por Corrado Gini en 1912.
Ejemplo – Curva de Lorenz Clásica. Para un ejemplo asegurador, la Figura 7.3 muestra una distribución de los siniestros de un seguro. Esta figura está basada en una muestra aleatoria de 2000 siniestros. El lado izquierdo muestra un histograma con asimetría por la derecha de los siniestros. El lado derecho proporciona la correspondiente curva de Lorenz, mostrando de nuevo una distribución asimétrica. Por ejemplo, la flecha marca el punto donde el 60 por ciento de los asegurados tienen el 30 por ciento de los siniestros. La línea de 45 grados es la línea de igualdad; si cada asegurado tuviera la misma siniestralidad, entonces la distribución de siniestralidad coincidiría con esta línea. El índice de Gini, dos veces la área entre la curva de Lorenz y la línea de 45 grados, es un 37.6 por ciento para este conjunto de datos.
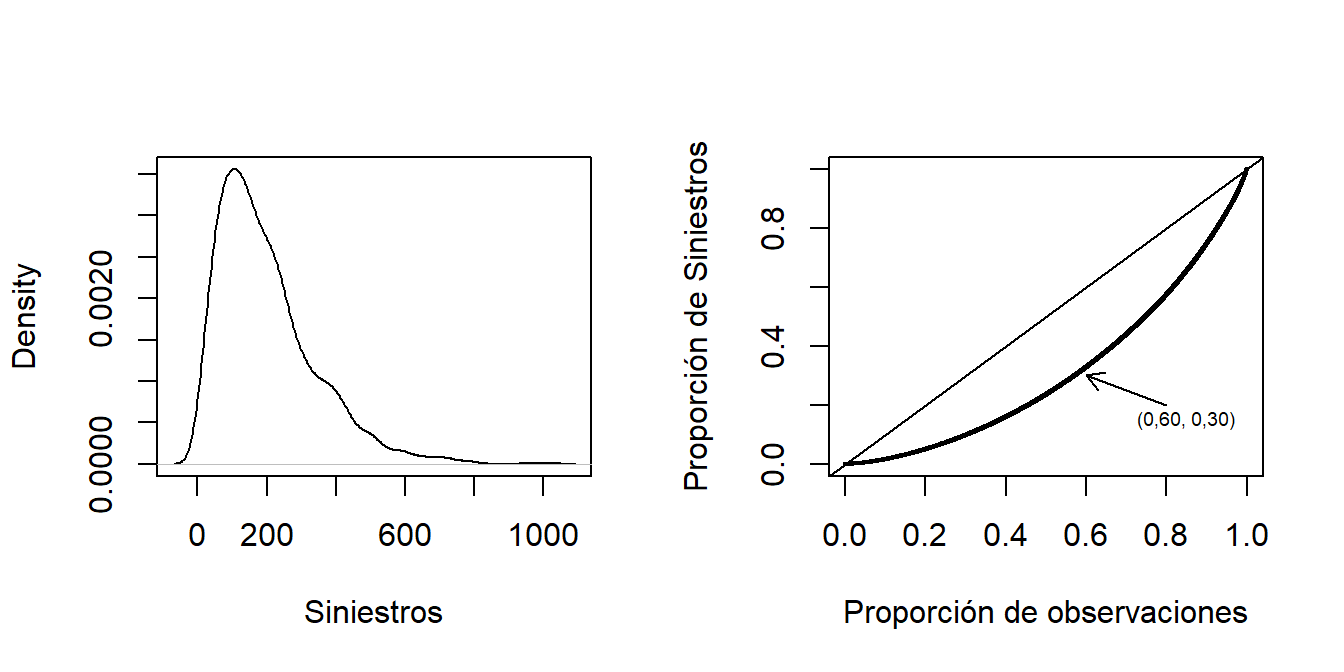
Figure 7.3: Distribución de los Siniestros de un Seguro. El lado izquierdo es la función de densidad de los siniestros. El lado derecho muestra los mismos datos mediante la curva de Lorenz.
7.6.2 Curva de Rendimiento y Estadístico de Gini
Ahora podemos introducir una modificación de la clásica curva de Lorenz y del índice de Gini que sea útil para aplicaciones del seguro. Específicamente, introducimos una curva de rendimiento que, en este caso, es un gráfico de la distribución de siniestros versus la de primas, donde ambas están ordenadas por prima. Para concretar ideas, proporcionamos alguna notación y consideramos \(i=1, \ldots, n\) pólizas. Para la \(i\)-ésima póliza,
- \(y_i\) denota el siniestro del seguro,
- \(\mathbf{x}_i\) es un conjunto de variables de tarificación conocidas por el analista, y \(P_i=P(\mathbf{x}_i)\) es la prima asociada, que es una función que depende de \(\mathbf{x}_i\).
El conjunto de información utilizada para calcular la curva de rendimiento para la \(i\)-ésima póliza es \((y_i, P_i)\).
Curva de rendimiento
En primer lugar, es conveniente ordenar el conjunto de pólizas según las primas (de más pequeñas a más grandes) y, a continuación, calcular las distribuciones de primas y siniestros. La distribución de primas es \[\begin{equation} \hat{F}_P(s) = \frac{ \sum_{i=1}^n P_i ~\mathrm{I}(P_i \leq s) }{\sum_{i=1}^n P_i} , \tag{7.5} \end{equation}\]
Y la distribución de siniestros es
\[\begin{equation} \hat{F}_{L}(s) = \frac{ \sum_{i=1}^n y_i ~\mathrm{I}(P_i \leq s) }{\sum_{i=1}^n y_i} , \tag{7.6} \end{equation}\]
donde \(\mathrm{I}(\cdot)\) es una función indicador, que devuelve 1 si el acontecimiento es cierto y cero en caso contrario. Para un valor dado \(s\), \(\hat{F}_P(s)\) nos da la proporción de primas menores o iguales a \(s\), y \(\hat{F}_{L}(s)\) nos da la proporción de siniestros para aquellos asegurados con primas menores o iguales a \(s\). El gráfico \(\left(\hat{F}_P(s),\hat{F}_{L}(s) \right)\) es conocido como *curva de rendimiento**.
Ejemplo – Distribución de Siniestralidad. Suponemos que tenemos \(n=5\) asegurados con el siguiente historial. Los datos han sido ordenados por primas.
| Variable | \(i\) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Prima | \(P(\mathbf{x}_i)\) | 2 | 4 | 5 | 7 | 16 |
| Primas Acumuladas | \(\sum_{j=1}^i P(\mathbf{x}_j)\) | 2 | 6 | 11 | 18 | 34 |
| Siniestralidad | \(y_i\) | 2 | 5 | 6 | 6 | 17 |
| Siniest. Acumul. | \(\sum_{j=1}^i y_j\) | 2 | 7 | 13 | 19 | 36 |
La Figura 7.4 compara la curva de Lorenz con la curva de rendimiento. En el lado izquierdo se muestra la curva de Lorenz. En el eje horizontal tenemos las proporciones acumuladas de asegurados (0, 0,2, 0,4, y en adelante) y en el eje vertical tenemos la proporción acumulada de siniestros (0, 2/36, 7/36, y en adelante). Para la curva de Lorenz, primero ordenamos por la cuantía del siniestro (lo que para este sencillo ejemplo representa lo mismo que ordenar por primas). Esta figura muestra una gran separación entre las distribuciones de siniestralidad y asegurados.
El lado derecho nos muestra la curva de rendimiento. Como las observaciones están ordenadas por prima, el primer punto después del origen (leyendo de izquierda a derecha) es (2/34, 2/36). El segundo punto es (6/34, 7/36). De la figura, vemos que hay poca separación entre siniestros y primas.
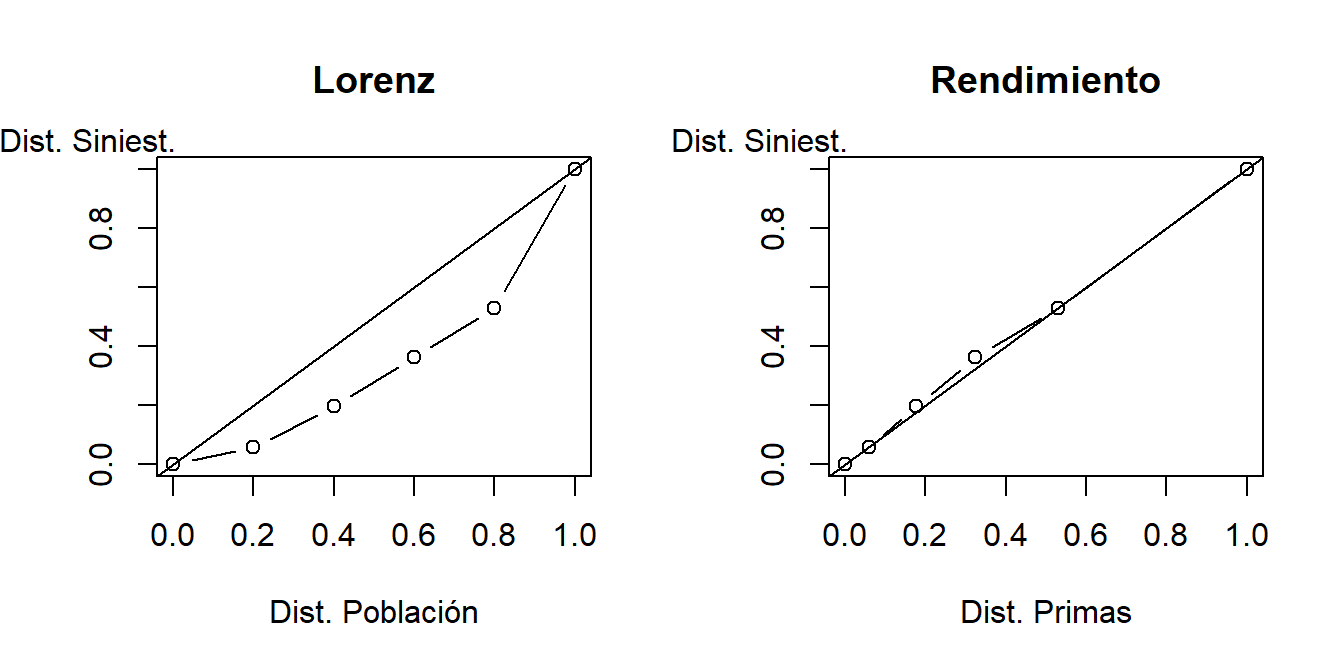
Figure 7.4: Curva Lorenz versus Curva Rendimiento
La curva de rendimiento puede ser útil al analista que trata de formar carteras rentables para el asegurador. Por ejemplo, supongamos que \(s\) es escogido para representar el percentil 95 de la distribución de primas. Entonces, el eje horizontal, \(\hat{F}_P(s)\), representa la fracción de primas para esta cartera y el eje vertical, \(\hat{F}_L(s)\), la fracción de siniestros para esta cartera. Cuando se plantean los principios de tarificación, los analistas buscan evitar situaciones no rentables y conseguir beneficios.
La esperanza del numerador en la ecuación (7.6) es \(\sum_{i=1}^n \mathrm{E}~ y_i=\sum_{i=1}^n \mu_i\). Así, si el principio de tarificación es escogido tal que \(P_i= \mu_i\), entonces esperaremos una relación muy próxima entre las distribuciones de prima y siniestralidad, resultando una línea de 45 grados. La línea de 45 grados iguala primas y siniestros, una situación de equilibrio que es una referencia para la tarificación de seguros.
Estadístico de Gini
La curva de Lorenz clásica muestra la proporción de asegurados en el eje horizontal y la función de distribución de la siniestralidad en el eje vertical. La curva de rendimiento extiende la curva de Lorenz clásica en dos maneras, (1) a través de la ordenación de riesgos y precios por primas y (2) permitiendo que los precios varíen por observación. Podemos resumir la curva de rendimiento de la misma manera que la curva de Lorenz clásica, utilizando un estadístico de Gini, definido como dos veces el área entre la curva y la línea de 45 grados. El analista busca las curvas de rendimiento que mejor se aproximen a la línea de 45 grados; éstas tienen menos separación entre las distribuciones de siniestros y primas y, por tanto, un estadístico de Gini menor.
Específicamente, el estadístico de Gini puede ser calculado como sigue. Suponemos que la curva de rendimiento empírica viene dada por \(\{ (a_0=0, b_0=0), (a_1, b_1), \ldots,\) \((a_n=1, b_n=1) \}\) para una muestra de \(n\) observaciones. Aquí, utilizamos \(a_j = \hat{F}_P(P_j)\) y \(b_j = \hat{F}_{L}(P_j)\). Entonces, el estadístico de Gini empírico es
\[\begin{eqnarray} \widehat{Gini} &=& 2\sum_{j=0}^{n-1} (a_{j+1} - a_j) \left \{ \frac{a_{j+1}+a_j}{2} - \frac{b_{j+1}+b_j}{2} \right\} \nonumber \\ &=& 1 - \sum_{j=0}^{n-1} (a_{j+1} - a_j) (b_{j+1}+b_j) . \tag{7.7} \end{eqnarray}\]
Mostrar Detalles de la Fórmula de Gini
Ejemplo – Distribución de Siniestralidad: Continuación. El estadístico de Gini para la curva de Lorenz (lado izquierdo de la Figura 7.4) es un 34.4 por ciento. En contraste, el estadístico de Gini para la curva de rendimiento (lado derecho) es un 1.7 por ciento.
7.6.3 Validación Cruzada
Los beneficios de la validación cruzada (out-of-sample validation, en inglés) para la selección de modelos fueron introducidos en la Sección 4.2. Ahora mostraremos el uso del estadístico de Gini y la curva de rendimiento en este contexto. El procedimiento sería:
- Usar la muestra de entrenamiento para la estimación de los diferentes modelos a comparar, cada uno produciendo una función de prima.
- Designar una muestra de validación a partir de \(\{(y_i, \mathbf{x}_i), i=1,\ldots,n\}\).
- Utilizar las variables explicativas de la muestra de validación para calcular las primas de la forma \(P(\mathbf{x}_i)\).
- Calcular el estadístico de Gini para cada modelo. Escoger el modelo con el menor estadístico de Gini.
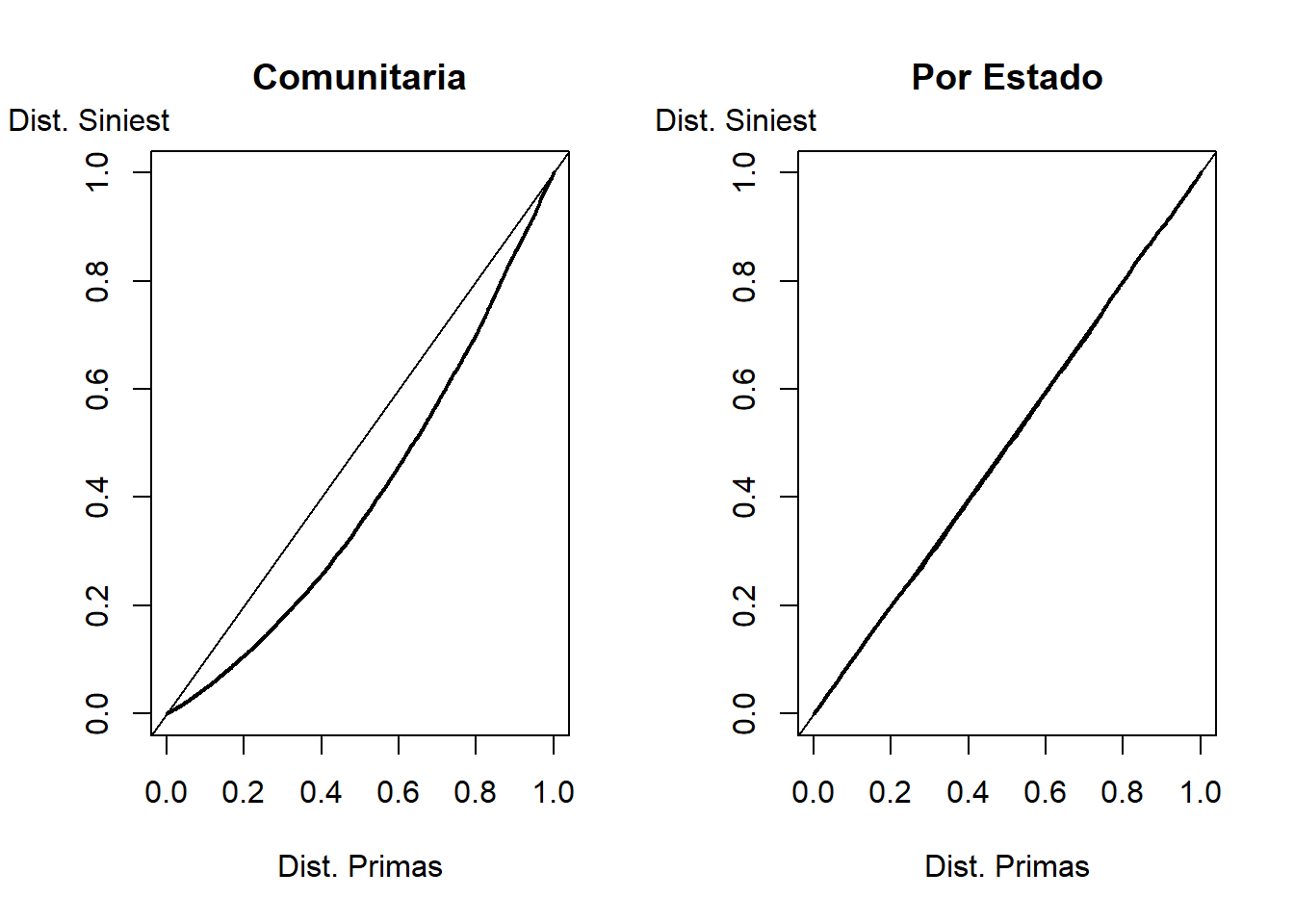
*Ejemplo – Tarificación Comunitaria versus Primas que Varían por Estado.** Suponemos que tenemos experiencia histórica de 25 estados y que, para cada estado, tenemos disponibles 200 observaciones que pueden servir para pronosticar siniestros futuros. Por simplicidad, suponemos que el analista conoce que estos siniestros siguen, o fueron generados por, una distribución gamma con un parámetro de forma común igual a 5. Desconocido para el analista, los parámetros de escala varían para cada estado, desde 20 a 66.
- Para calcular las primas de base, el analista supone un parámetro de escala que es común para todos los estados y que se estima a partir de los datos. Podemos pensar de esta prima común como una prima basada en un principio de tarificación comunitaria.
- Como alternativa, el analista deja que los parámetros de escala varíen para cada estado y otra vez utilizará los datos para estimar dichos parámetros.
Una muestra de validación de 100 siniestros está disponible para cada estado. Para cada uno de los dos procedimientos de tarificación, determinar la curva de rendimiento y el correspondiente estadístico de Gini. Escoger el procedimiento de tarificación con el menor estadístico de Gini.
Solución del Ejemplo
Discusión
En la modelización de los siniestros de seguros, las medidas estándar de validación cruzada no son las más informativas debido a las altas proporciones de ceros (pólizas con ninguna reclamación) y a la alta asimetría de la distribución para los valores positivos. En contraste, el estadístico de Gini funciona muy bien en presencia de muchos ceros (véase la demostración en (Edward W. Frees, Meyers, and Cummings 2014)).
El valor de las curvas de rendimiento y los estadísticos de Gini han sido recientemente tratadas en el artículo de Denuit, Sznajder, and Trufin (2019). Las propiedades de una versión extendida, tratando con relatividades para las primas nuevas, fue desarrollada por Frees, Meyers, and Cummings (2011) y Edward W. Frees, Meyers, and Cummings (2014). En estos artículos se pueden encontrar las fórmulas para los errores estándares y otra información adicional.
7.7 Otros Recursos y Colaboradores
Este capítulo sirve como puente entre la introducción técnica de este libro y una introducción a la tarificación llevada a cabo por los actuarios en la práctica. Para los lectores interesados en aprender aspectos prácticos de la tarificación, recomendamos las introducciones de la Society of Actuaries en Friedland (2013) y por la Casualty Actuarial Society en Werner and Modlin (2016). Para una introducción clásica de la gestión del riesgo para la tarificación, véase Niehaus and Harrington (2003). Véase también Finger (2006) y Edward W Frees (2014).
Bühlmann (1985) fue el primero en la literatura académica en argumentar que la tarificación debería ser hecha primero a nivel de la cartera (se refería a esto como aproximación top down) para, posteriormente, ser ajustada a nivel de los contratos individuales. Véase también la discusión en Kaas et al. (2008), Capítulo 5.
Para más referencias sobre los principios de tarificación, un tratamiento clásico es Gerber (1979) y una aproximación más moderna es Kaas et al. (2008). Para una discusión desde un punto de vista económico-financiero, véase Bauer, Phillips, and Zanjani (2013).
- Edward W. (Jed) Frees, University of Wisconsin-Madison, y José Garrido, Concordia University son los autores principales de la versión inicial de este capítulo. Email: jfrees@bus.wisc.edu y/o jose.garrido@concordia.ca para comentarios del capítulo y sugerencias de mejora.
- Revisores de los capítulos, entre otros: escribir a Jed o José para añadir su nombre aquí.
- Traducción al español: Lluís Bermúdez (Universitat de Barcelona)
TS 7.A. Regulación de la Tarificación
La regulación del seguro es necesaria para asegurar la estabilidad financiera de los aseguradores y para proteger a los consumidores. Los aseguradores reciben unas primas a cambio de las promesas de pagar en caso de ocurrencia del evento asegurado. Como en otras instituciones financieras, como los bancos, hay un fuerte interés público en promover la viabilidad económica futura de los aseguradores.
Conducta de mercado
<!— Uno de los aspectos de regulación es conocido como regulación de la conducta del mercado - sistemas de control regulatorios que han sido establecidos como requerimiento a los aseguradores para demostrar que están proporcionando unos servicios justos y fiables, incluyendo la regulación del producto. –>
Para ayudar a proteger a los consumidores, los reguladores imponen unas reglas administrativas sobre el comportamiento de los participantes en el mercado. Estas reglas, conocidas como regulación de conductas de mercado, proporcionan sistemas de control regulatorios que disponen que los aseguradores deben demostrar que están proporcionando servicios justos y fiables, incluyendo la tarificación, de acuerdo con los estatutos y controles de una jurisdicción.
- La regulación de producto sirve para proteger a los consumidores asegurando que las provisiones de las pólizas de seguro son razonables y justas, y que no presentan vacíos importantes en cuanto a la cobertura que podrían ser mal entendidos por los consumidores y dejarles desprotegidos.
- El producto asegurador es el contrato de seguro (póliza) y la cobertura que proporciona. Los contratos de seguro están regulados por las siguientes razones:
- Las pólizas de seguro son documentos legales complejos que a menudo son difíciles de interpretar y entender.
- Los aseguradores definen pólizas y las venden al público en un “o lo tomas o lo dejas”.
La conducta de mercado incluye reglas para los mediadores como agentes (quiénes principalmente venden seguros a particulares) y corredores (quiénes principalmente venden seguros a empresas). La conducta de mercado también incluye regulación de normas de competencia, diseñada para asegurar un mercado eficaz y competitivo que ofrezca buenas ofertas a los consumidores.
Regulación de Tarifa
La regulación de tarifa sirve de guía en el desarrollo de las primas y por ello es el aspecto principal de este capítulo. Como otros aspectos del control de conducta de mercado, la intención de estas regulaciones es asegurarse que los aseguradores no se benefician injustamente de los consumidores. La regulación de la tarifa (y de la forma de la póliza) es común en todo el mundo.
El grado de regulación varía según el producto de seguro. La regulación de la tarifa es poco común en los seguros de vida. Además, algunos seguros de no-vida, como los ramos más empresariales y el reaseguro, la tarifa está libre de control. La regulación de tarifa es común en el seguro de automóvil, el seguro de salud, los seguros de accidentes laborables, el seguro de responsabilidad civil médica y el seguro de hogar. Estos son mercados en que el seguro es obligatorio o en el que socialmente es deseable una cobertura universal.
Hay tres principios que guían la regulación de tarifa. Las tarifas tienen que:
- ser adecuadas (para mantener la solvencia de la compañía aseguradora),
- pero no excesivas (no tan alta para producir beneficios desorbitados),
- ni injustamente discriminatoria (las diferencias de precio solo deben reflejar diferencias en gastos y reclamaciones esperadas).
Recientemente, en los seguros de hogar y automóvil, los temas entrelazados de disponibilidad y accesibilidad, no incluidos explícitamente en los anteriores principios, han ido tomando más importancia en las decisiones regulatorias.
Las Tarifas no son Injustamente Discriminatorias
Algunas regulaciones gubernamentales del seguro restringen la cantidad, o nivel, de las tarifas o primas. Estas regulaciones tratan de conseguir los dos primeros de los tres principios de la regulación sobre tarificación, esto es, que las tarifas deben ser adecuadas pero no excesivas. Este tipo de regulación será discutida en la sección siguiente sobre tipos de regulación tarifaria.
En el seguro de vida, desde hace mucho tiempo ha sido aceptado que es razonable y justo cobrar primas de tarifa diferentes por edad. Por ejemplo, una prima de un seguro de vida difiere dramáticamente entre una persona de 80 años y otra de 20 años. En contraste, no está aceptado utilizar tarifas que difieran por:
- Etnia/raza,
- Afiliación política, o
- Religión.
No importa si estos datos pueden ser usados para establecer una significación estadística entre las categorías de cualquiera de estas tres variables. Lo relevante es la decisión social sobre qué se considera como concepto de “justicia.”
Diferentes jurisdicciones han tomado diferentes posturas sobre qué constituye una variable de tarificación justa. Por ejemplo, en algunas jurisdicciones, para algunos productos aseguradores, el género ya no es una variable permitida. Por ejemplo, en la Unión Europea está prohibido el uso del género del asegurado para el cálculo de las primas. Como otro ejemplo, en los EE.UU., mucho se ha discutido sobre si permitir el uso del índice de crédito del asegurado en la tarifa de su seguro de automóvil. Los índices de crédito están diseñados para medir el grado de responsabilidad financiera del consumidor. En este sentido, algunos argumentan que estos índices de crédito sirven como aproximación de la etnicidad del asegurado y, por tanto, deberían estar prohibidos.
En una época donde los datos están siendo utilizados de múltiples maneras imaginativas, la discusión sobre qué variable constituye una variable justa queda fuera del alcance de este texto. Aun así, es pertinente remarcar que los actuarios y otros analistas de datos pueden contribuir a las discusiones sociales sobre qué constituye una variable de tarificación “justa”, concretamente, determinando la magnitud de las diferencias de precio cuando se utilizan las variables bajo discusión.
<!—¿Debemos recoger estas variables? –>
Tipos de Regulación Tarifaria
Hay varios métodos, que varían según el nivel regulatorio, con los que los reguladores pueden restringir las tarifas que ofrecen los aseguradores.
El más restrictivo es un sistema regulador de prescripción gubernamental, donde el regulador gubernamental determina y decreta las tarifas, las clasificaciones, la forma, y otras particularidades a las que todos los aseguradores tienen que adherirse. También de carácter restrictivo es un sistema de aprobación previa. En este caso, el asegurador debe presentar las tarifas, las normas y el resto de información requerida por el regulador. Según la normativa, la documentación presentada se considera efectiva tras la finalización de un periodo de tiempo determinado (si el regulador no realiza una acción concreta sobre la documentación presentada, se considera aprobada automáticamente) o cuando el regulador la aprueba formalmente.
El menos restrictivo es un sistema de no presentación o de mantenimiento de registro donde el asegurador no necesita presentar documentación sobre tarifas, normas y otros requerimientos al regulador. El regulador periódicamente puede examinar al asegurador para comprobar que actúa con conformidad a la ley. Otro sistema relativamente flexible es el sistema de presentación única, también conocido como tarificación competitiva, donde el asegurador sencillamente debe mantener unos documentos para asegurar su conformidad con la ley.
Entre estos dos extremos encontramos (1) presentación y uso, (2) uso y presentación, (3) aprobación previa modificada, y (4) sistemas flexibles de tarifa.
- Presentación y Uso: El asegurador debe presentar documentación sobre tarifas, normas y otros requerimientos al regulador. Los términos de la documentación son efectivos inmediatamente o tras finalizar un periodo especificado por el regulador.
- Uso y Presentación: El asegurador debe presentar documentación sobre tarifas, normas y otros requerimientos al regulador dentro de un periodo de tiempo especificado después de su primer uso. Los términos de la documentación son efectivos al ser utilizados.
- Aprobación Previa Modificada: Esto es un híbrido entre los sistemas de “aprobación previa” y de “presentación y uso”. Si la revisión de la tarifa sólo responde a un cambio en la experiencia histórica, aplica el sistema de “presentación y uso”. Sin embargo, si la revisión de tarifa responde a un cambio en los recargos de gastos o en las clasificaciones de la tarifa, entonces aplica la “aprobación previa”.
- Tarifa Flexible (o Franja Tarifaria): El asegurador puede aumentar o disminuir la tarifa dentro de una “franja flexible,” o rango, sin aprobación del regulador. Generalmente, aquí puede aplicar un sistema de “presentación y uso” o bien de “uso y presentación”.
Para una profunda revisión de la regulación aseguradora desde una perspectiva global, véase la página web de la Asociación Internacional de Reguladores de Seguro (IAIS, en sus siglas en inglés).
Bibliography
Bauer, Daniel, Richard D. Phillips, and George H. Zanjani. 2013. “Financial Pricing of Insurance.” In Handbook of Insurance, 627–45. Springer.
Denuit, Michel, Dominik Sznajder, and Julien Trufin. 2019. “Model Selection Based on Lorenz and Concentration Curves, Gini Indices and Convex Order.” Insurance: Mathematics and Economics.
Finger, Robert J. 2006. “Risk Classification.” In Foundations of Casualty Actuarial Science, 231–76.
Frees, Edward W. 2014. “Frequency and Severity Models.” In Predictive Modeling Applications in Actuarial Science, edited by Edward W Frees, Glenn Meyers, and Richard Derrig, 1:138–64. Cambridge University Press Cambridge.
Frees, Edward W., Glenn Meyers, and A. David Cummings. 2011. “Summarizing Insurance Scores Using a Gini Index.” Journal of the American Statistical Association 106 (495): 1085–98.
Frees, Edward W., Glenn Meyers, and A. David Cummings. 2011. “Summarizing Insurance Scores Using a Gini Index.” Journal of the American Statistical Association 106 (495): 1085–98.
2014. “Insurance Ratemaking and a Gini Index.” Journal of Risk and Insurance 81 (2): 335–66.Friedland, Jacqueline. 2013. Fundamentals of General Insurance Actuarial Analysis. Society of Actuaries.
Gerber, Hans U. 1979. An Introduction to Mathematical Risk Theory, Vol. 8 of Ss Heubner Foundation Monograph Series. University of Pennsylvania Wharton School SS Huebner Foundation for Insurance Education.
Kaas, Rob, Marc Goovaerts, Jan Dhaene, and Michel Denuit. 2008. Modern Actuarial Risk Theory: Using R. Vol. 128. Springer Science & Business Media.
Lorenz, Max O. 1905. “Methods of Measuring the Concentration of Wealth.” Publications of the American Statistical Association 9 (70): 209–19.
Niehaus, Gregory, and Scott Harrington. 2003. Risk Management and Insurance. New York: McGraw Hill.
Werner, Geoff, and Claudine Modlin. 2016. Basic Ratemaking, Fifth Edition. Casualty Actuarial Society. https://www.casact.org/library/studynotes/werner_modlin_ratemaking.pdf.