Chapter 3 Modelización de la Severidad de las Pérdidas

Vista previa del capítulo. El enfoque tradicional para la modelización de la distribución de las pérdidas agregadas comienza ajustando por separado una distribución para la frecuencia al número de pérdidas y una distribución para la severidad al tamaño de las pérdidas. La distribución de pérdidas agregades estimada combina la distribución para la frecuencia y la distribución para la severidad de las pérdidas por convolución. En el Capítulo 2 han sido utilizadas distribuciones discretas, frecuentemente referenciades como distribuciones para el recuento o distribuciones para la frecuencia, para describir el número de eventos, como por ejemplo el número de accidentes del conductor o número de siniestros del asegurado. Tiempos de vida, valores de activos, pérdidas y tamaños de siniestros son frecuentemente modelizados como variables aleatorias continuas y como tales son modelizadas usando distribuciones continuas, frecuentemente referenciades como distribuciones de perdidas o de severidad. Una distribución mixta es una combinación ponderada de distribuciones más simples que es usada para modelitzar un fenómeno investigado en una población heterogénea, como modelitzar más de un tipo de siniestro en el seguro de responsabilidad civil (siniestros pequeños pero frecuentes y siniestros grandes pero relativamente raros). En este capítulo se explora el uso de distribuciones continuas y mixtas para modelitzar el tamaño aleatorio de las pérdidas. Se presentan atributos clave que caracterizan modelos continuos y que además son un medio para crear nuevas distribuciones a partir de otras existentes. También se explora el efecto de modificaciones de cobertura, que cambian las condiciones que desencadenan el pago, como por ejemplo la aplicación de franquicias, límites, o ajustes por inflación, a la distribución de las cantidades de pérdidas individuales. Las distribuciones de frecuencias del Capítulo 2 seran combinadas con las ideas de este capítulo para describir las pérdidas agregadas del conjunto de la cartera en el Capítulo 5.

3.1 Cantidades Distribucionales Básicas

---

En esta sección, se muestra la definición de algunas cantidades distribucionales básicas:

• momentos,
• percentiles, y
• funciones generadoras.

---

3.1.1 Momentos

Sea \(X\) una variable aleatoria continua con función de densidad de probabilidad \(f_{X}\left( x \right)\). El k-ésimo momento ordinario de \(X\), denotado como \(\mu_{k}^{\prime}\), es el valor esperado de la k-esima potencia de \(X\), siempre que esta exista. El primer momento ordinario \(\mu_{1}^{\prime}\) es la media de \(X\) frecuentemente denotada como \(\mu\). La fórmula para \(\mu_{k}^{\prime}\) viene dada por \[ \mu_{k}^{\prime} = \mathrm{E}\left( X^{k} \right) = \int_{0}^{\infty}{x^{k}f_{X}\left( x \right)dx } . \] El soporte de la variable aleatoria \(X\) se asume que es no negativo dado que los fenómenos actuariales son raramente negativos. Una simple integración por partes demuestra que los momentos ordinarios para variables no negativas pueden también calcularse usando \[ \mu_{k}^{\prime} = \int_{0}^{\infty}{k~x^{k-1}\left[1- F_{X}(x) \right]dx }, \] que está basado en la función de supervivencia, denotada como \(S_X(x) = 1-F_{X}(x)\). Esta fórmula es particularment útil cuando \(k=1\).

El k-ésimo momento central de \(X\), denotado como \(\mu_{k}\), es el valor esperado de la potencia k-ésima de la desviación de \(X\) respecto de su media \(\mu\). La fórmula para \(\mu_{k}\) viene dada por \[ \mu_{k} = \mathrm{E}\left\lbrack {(X - \mu)}^{k} \right\rbrack = \int_{0}^{\infty}{\left( x - \mu \right)^{k}f_{X}\left( x \right) dx }. \] El segundo momento central \(\mu_{2}\) define la varianza de \(X\), denotada por \(\sigma^{2}\). La raíz cuadrada de la varianza es la desviación estándar \(\sigma\).

Desde una perspectiva clásica, otras caracterizaciones de la forma de una distribución incluyen su grado de simetria así como su apuntamiento en comparación con la distribución normal. La ratio del tercer momento central sobre el cubo de la desviación estándar \(\left( \mu_{3} / \sigma^{3} \right)\) define el coeficiente de asimetría que es una medida de simetría. Un coeficiente positivo de asimetria indica que la distribución es asimétrica por la derecha (asimetria positiva). La ratio del cuarto momento central sobre la cuarta potencia de la desviación estándar \(\left(\mu_{4} / \sigma^{4} \right)\) define el coeficiente de curtosis. La distribución normal tiene un coeficiente de curtosis de 3. Una distribución con un coeficiente de curtosis mayor que 3 tiene colas más pesadas y un mayor pico que la normal, mientras que distribuciones con un coeficiente de curtosis menor que 3 tienen colas más ligeras y son más planas. En la Sección 10.2 se describen las colas de las distribuciones desde una perspectiva actuarial y aseguradora.

Ejemplo 3.1.1. Pregunta de un examen actuarial. Asumimos que la v.a. \(X\) tiene una distribución gamma con media 8 y asimetría 1. Determina la varianza de \(X\). (Hint: La distribución gamma es tratada en la Sección 3.2.1.)

Mostrar Solución de Ejemplo

Solución. La función de densidad de probabilidad de \(X\) viene dada por \[ f_{X}\left( x \right) = \frac{\left( x / \theta \right)^{\alpha}}{x ~\Gamma\left( \alpha \right)} e^{- x / \theta} \] para \(x > 0\). Para \(\alpha>0\), el k-ésimo momento ordinário es \[ \mu_{k}^{\prime} = \mathrm{E}\left( X^{k} \right) = \int_{0}^{\infty}{\frac{1}{\Gamma\left( \alpha \right)\theta^{\alpha}}x^{k + \alpha - 1}e^{- x / \theta} dx} = \frac{\Gamma\left( k + \alpha \right)}{\Gamma\left( \alpha \right)}\theta^{k} \] Dado que \(\Gamma\left( r + 1 \right) = r\Gamma\left( r \right)\) y \(\Gamma\left( 1 \right) = 1\), then \(\mu_{1}^{\prime} = \mathrm{E}\left( X \right) = \alpha\theta\), \(\mu_{2}^{\prime} = \mathrm{E}\left( X^{2} \right) = \left( \alpha + 1 \right)\alpha\theta^{2}\), \(\mu_{3}^{\prime} = \mathrm{E}\left( X^{3} \right) = \left( \alpha + 2 \right)\left( \alpha + 1 \right)\alpha\theta^{3}\), y \(\mathrm{Var}\left( X \right) = (\alpha + 1)\alpha\theta^2 - (\alpha\theta)^2 = \alpha\theta^{2}\).

\[ \text{Skewness} = \frac{\mathrm{E}\left\lbrack {(X - \mu_{1}^{\prime})}^{3} \right\rbrack}{{\mathrm{Var}\left( X \right)}^{3/2}} = \frac{\mu_{3}^{\prime} - 3\mu_{2}^{\prime}\mu_{1}^{\prime} + 2{\mu_{1}^{\prime}}^{3}}{{\mathrm{Var}\left( X \right)}^{3/2}} \\ = \frac{\left( \alpha + 2 \right)\left( \alpha + 1 \right)\alpha\theta^{3} - 3\left( \alpha + 1 \right)\alpha^{2}\theta^{3} + 2\alpha^{3}\theta^{3}}{\left( \alpha\theta^{2} \right)^{3/2}} = \frac{2}{\alpha^{1/2}} = 1. \]

Por lo tanto, \(\alpha = 4\). Dado que \(\mathrm{E}\left( X \right) = \alpha\theta = 8\), entonces \(\theta = 2\) y finalmente, \(\mathrm{Var}\left( X \right) = \alpha\theta^{2} = 16\).

---

3.1.2 Cuantiles

Los cuantiles también pueden ser usados para describir las características de la distribución de \(X\). Cuando la distribución de \(X\) es continua, para una fracción concreta \(0 \leq p \leq 1\) el correspondiente cuantil es la solución a la ecuación \[ F_{X}\left( \pi_{p} \right) = p . \] Por ejemplo, el punto medio de una distribución, \(\pi_{0.5}\), es la mediana. Un percentil es un tipo de cuantil; un \(100p\) percentil es el número tal que \(100 \times p\) porciento de los datos están por debajo de él.

Ejemplo 3.1.1. Pregunta de un examen actuarial. Sea \(X\) una variable aleatoria continua con función de densidad \(f_{X}\left( x \right) = \theta e^{- \theta x}\), para \(x > 0\) y 0 en caso contrario. Si la mediana de la distribución es \(\frac{1}{3}\), encuentra \(\theta\).

Mostrar Solución de Ejemplo

Solución.

La función de distribución es \(F_{X}\left( x \right) = 1 - e^{- \theta x}\). Por tanto, \(F_{X}\left( \pi_{0,5} \right) = 1 - e^{- \theta\pi_{0.5}} = 0.5\). Como \(\pi_{0,5} = \frac{1}{3}\), tenemos que \(F_X\left(\frac{1}{3}\right) = 1 - e^{-\theta / 3} = 0,5\) y \(\theta = 3 \ln 2\).

---

En la Sección 4.1.1.3 se extiende la definición de cuantil para incluir las distribuciones que son discretas, continuas, o una combiación híbrida.

3.1.3 Función generatriz de momentos

La función generatriz de momentos, denotada por \(M_{X}(t)\) caracteriza unícovamente la distribución de \(X\). Mientras que es posible que dos distribuciones diferentes tengan los mismos momentos y sigan siendo diferentes, esto no ocurre con la función generatriz de momentos. Es decir, si dos variables aleatorias tienen la misma función generatriz de momentos, entonces tienen la misma distribución. La función generatriz de momentos viene dada por \[ M_{X}(t) = \mathrm{E}\left( e^{tX} \right) = \int_{0}^{\infty}{e^{\text{tx}}f_{X}\left( x \right) dx } \] para todo \(t\) para el que exista el valor esperado. La función generatriz de momentos es una función real para la que la k-ésima derivada en cero es igual al k-ésimo momento ordinario de \(X\). En símbolos, esto es \[ \left.\frac{d^k}{dt^k} M_{X}(t)\right|_{t=0} = \mathrm{E}\left( X^{k} \right) . \]

Ejemplo 3.1.3. Pregunta de un examen actuarial. La variable aleatoria \(X\) tiene una distribución exponencial con media \(\frac{1}{b}\). Se determina que \(M_{X}\left( - b^{2} \right) = 0,2\). Encuentra \(b\). (Hint: La exponencial es un caso especial de la distribución gamma que es tratada en la Sección 3.2.1.)

Mostrar Solución de Ejemplo

Solución.

Dado que \(X\) sigue una distribución exponencial con media \(\frac{1}{b}\), tenemos que \[ M_{X}(t) = \mathrm{E}\left( e^{tX} \right) = \int_{0}^{\infty}{e^{\text{tx}}be^{- bx} dx} = \int_{0}^{\infty}{be^{- x\left( b - t \right)} dx} = \frac{b}{\left( b - t \right)}. \]

Entonces, \[ M_{X}\left( - b^{2} \right) = \frac{b}{\left( b + b^{2} \right)} = \frac{1}{\left( 1 + b \right)} = 0,2. \] Por tanto, \(b = 4\).

---

Ejemplo 3.1.4. Pregunta de examen actuarial. Sea \(X_{1}, \ldots, X_{n}\) variables aleatorias independientes, donde \(X_i\) sigue una distribución gamma con parámetros \(\alpha_{i}\) y \(\theta\). Encuentra la distribución de \(S = \sum_{i = 1}^{n}X_{i}\), la media \(\mathrm{E}(S)\) y la varianza \(\mathrm{Var}(S)\).

Mostrar Solución de Ejemplo

Solución.

La función generatriz de momentos de \(S\) es \[ M_{S}(t) = \text{E}\left( e^{\text{tS}} \right) = \mathrm{E}\left( e^{t\sum_{i = 1}^{n}X_{i}} \right) = \mathrm{E}\left( \prod_{i = 1}^{n}e^{tX_{i}} \right) . \] Teniendo en cuenta que son independientes, obtenemos
\[ M_{S}(t) = \prod_{i = 1}^{n}{\mathrm{E}\left( e^{tX_{i}} \right) = \prod_{i = 1}^{n}{M_{X_{i}}(t)}} . \]

La función generatriz de momentos de una distribución gamma \(X_i\) es \(M_{X_i}(t) = (1-\theta)^{\alpha_i}\). . Entonces, \[ M_{S}(t) = \prod_{i = 1}^{n}\left( 1 - \theta t \right)^{- \alpha_{i}} = \left( 1 - \theta t \right)^{- \sum_{i = 1}^{n}\alpha_{i}} . \] Esto indica que la distribución de \(S\) es gamma con parámetros \(\sum_{i = 1}^{n}\alpha_{i}\) y \(\theta\).

Esta es una demostración de cómo puede usarse la propiedad de unicidad de la función generatriz de momentos para determinar la distribución de probabilidad de una variable aleatoria.

Podemos encontrar la media y varianza a partir de las propiedades de la distribución gamma. Alternativamente, determinando la primera y segunda derivadas de \(M_{S}(t)\) en cero, se demuestra que \(\mathrm{E}\left( S \right) = \left. \ \frac{\partial M_{S}(t)}{\partial t} \right|_{t = 0} = \alpha\theta\) donde \(\alpha = \sum_{i = 1}^{n}\alpha_{i}\), y \[ \mathrm{E}\left( S^{2} \right) = \left. \ \frac{\partial^{2}M_{S}(t)}{\partial t^{2}} \right|_{t = 0} = \left( \alpha + 1 \right)\alpha\theta^{2}. \] Por lo tanto, \(\mathrm{Var}\left( S \right) = \alpha\theta^{2}\).

---

También se puede usar la función generatriz de momentos para calcular la función generatriz de probabilidad

\[ P_{X}(z) = \mathrm{E}\left( z^{X} \right) = M_{X}\left( \ln z \right) . \]

Tal y como se introdujo en la Sección 2.2.2, la función generatriz de probabilidad es más útil para v.a.s discretas.

3.2 Distribuciones Continuas para Modelizar la Severidad de las Pérdidas

---

En esta sección, se presentará la definición y aplicación de cuatro distribuciones fundamentales para la severidad:

• gamma,
• Pareto,
• Weibull, y
• distribución beta generalitzada de segundo tipo.

---

3.2.1 Distribución gamma

El enfoque tradicional para la modelización de las pérdidas consiste en ajustar de forma separada modelos para la frecuencia y la severidad. Cuando la frecuencia y la severidad se modelizan por separado es común para los actuarios usar la distribución de Poisson (introducida en la Sección 2.2.3.2) para la frecuencia de siniestros y la distribucíon gamma para la severidad. Un enfoque alternativo para modelitzar las pérdidas que ha ganado popularidad recientemente es crear un único modelo para la prima pura (coste medio de los siniestros) que será descrito en el Capítulo Chapter 4.

Se dice que la variable continua \(X\) tiene una distribución gamma con parámetro de forma \(\alpha\) y parámetro de escala \(\theta\) si su función de densidad de probabilidad viene dada por \[ f_{X}\left( x \right) = \frac{\left( x/ \theta \right)^{\alpha}}{x~ \Gamma\left( \alpha \right)}\exp \left( -x/ \theta \right) \ \ \ \text{for } x > 0 . \] Nótese que \(\alpha > 0,\ \theta > 0\).

Los dos paneles de la Figura 3.1 muestran los efectos de los parámetros de escala y forma en la función de densidad de la gamma.

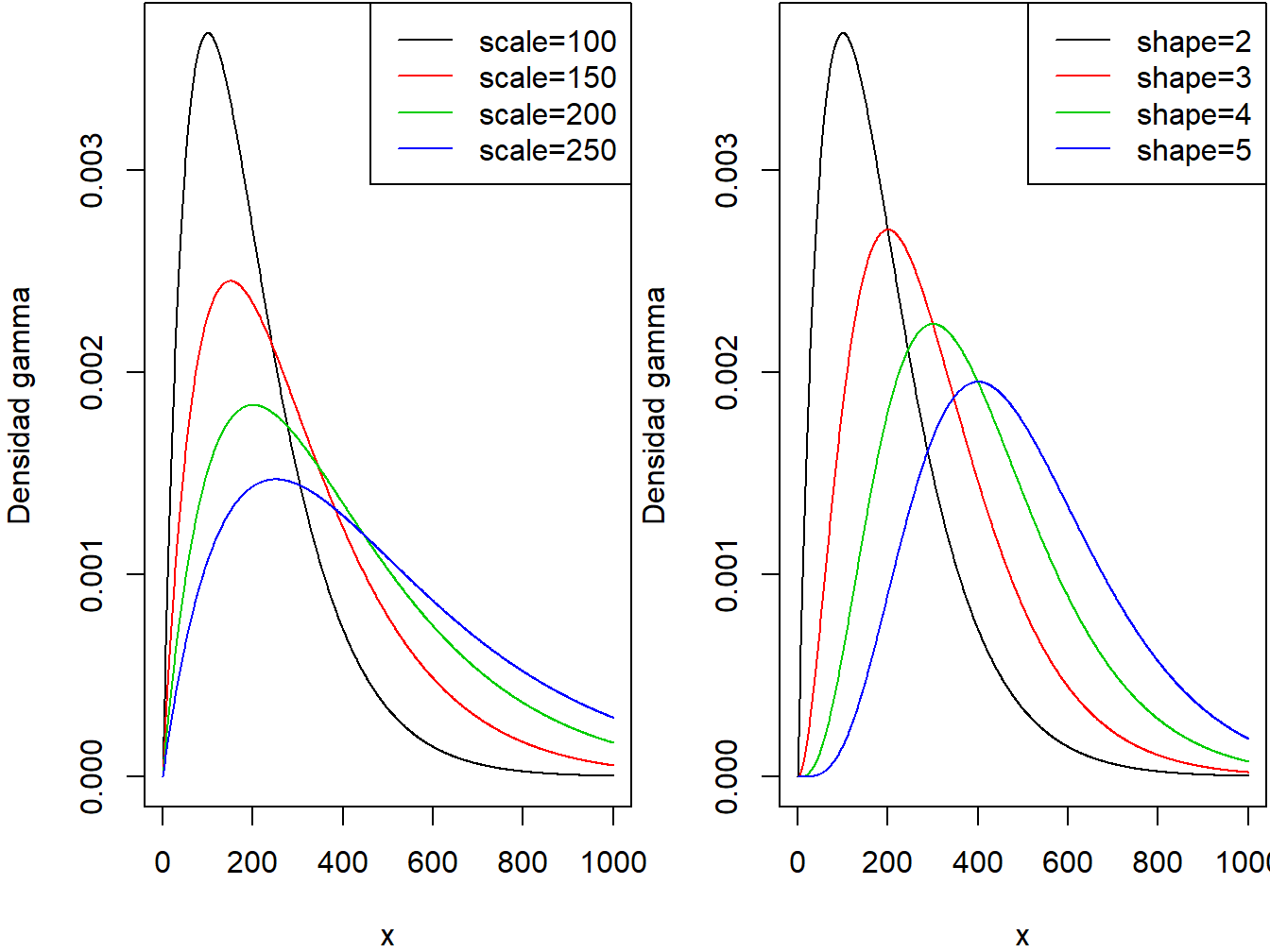
Figure 3.1: Densidades Gamma. El panel de la izquierda corresponde a forma=2 y un parámetro de escala variable. El panel de la derecha corresponde a escala=100 y parámetro de forma variable.

Código R para gráficos de densidad gamma

par(mfrow=c(1, 2), mar = c(4, 4, .1, .1))

# Densidades gamma con escala variable
scaleparam <- seq(100, 250, by = 50)
shapeparam <- 2:5
x <- seq(0, 1000, by = 1)
fgamma <- dgamma(x, shape = 2, scale = scaleparam[1])
plot(x, fgamma, type = "l", ylab = "Densidad gamma")
for(k in 2:length(scaleparam)){
  fgamma <- dgamma(x,shape = 2, scale = scaleparam[k])
  lines(x,fgamma, col = k)
}
legend("topright", c("scale=100", "scale=150", "scale=200", "scale=250"), lty=1, col = 1:4)

# Densidades gamma con forma variable
fgamma <- dgamma(x, shape = shapeparam[1], scale = 100)
plot(x, fgamma, type = "l", ylab = "Densidad gamma")
for(k in 2:length(shapeparam)){
  fgamma <- dgamma(x,shape = shapeparam[k], scale = 100)
  lines(x,fgamma, col = k)
}
legend("topright", c("shape=2", "shape=3", "shape=4", "shape=5"), lty=1, col = 1:4)

Cuando \(\alpha = 1\) la gamma se reduce a una distribución exponencial y cuando \(\alpha = \frac{n}{2}\) y \(\theta = 2\) la gamma se reduce a una distribucióin chi-cuadrado con \(n\) grados de libertad. Tal y como veremos en la Sección 15.4, la distribución chi-cuadrado es ampliamente utilitzada en el contraste estadístico de hipótesis.

La función de distribución de un modelo gamma es la función incompleta gamma, denotada por \(\Gamma\left(\alpha; \frac{x}{\theta} \right)\), y definida como \[ F_{X}\left( x \right) = \Gamma\left( \alpha; \frac{x}{\theta} \right) = \frac{1}{\Gamma\left( \alpha \right)}\int_{0}^{x /\theta}t^{\alpha - 1}e^{- t}~dt \] \(\alpha > 0,\ \theta > 0\). Para un entero \(\alpha\), puede expresarse como \(\Gamma\left( \alpha; \frac{x}{\theta} \right) = 1 - e^{-x/\theta}\sum_{k = 0}^{\alpha-1}\frac{(x/\theta)^k}{k!}\).

El momento \(k\)-ésimo de una variable aleatoria con distribución gamma para cualquier \(k\) positivo viene dada por \[ \mathrm{E}\left( X^{k} \right) = \theta^{k} \frac{\Gamma\left( \alpha + k \right)}{\Gamma\left( \alpha \right)} . \] La media y varianza vienen dadas por \(\mathrm{E}\left( X \right) = \alpha\theta\) y \(\mathrm{Var}\left( X \right) = \alpha\theta^{2}\), respectivamente.

Dado que todos los momentos existen para cualquier \(k\) positivo, la distribución gamma se considera una distribución de cola ligera, que puede no ser adecuada para modelitzar activos con riesgo dado que no proporciona una valoración realista de la versimilitud de pérdidas severas.

3.2.2 Distribución Pareto

La distribución Pareto, denominada así por el economista italiano Vilfredo Pareto (1843-1923), tiene muchas aplicacions económicas y financieras. Es una distribución con asimetria positiva y con cola pesada que la hace adecuada para modelitzar ingresos, siniestros en seguros con alto riesgo y la severidad de grandes pérdidas en seguros. La función de supervivencia de una distribución de Pareto que decrece lentamente a cero fue por primera vez utilizada para describir la distribución de ingresos en los que un pequeño porcentaje de la población tiene una gran proporción de la riqueza total. Para siniestros extermos en seguros, la cola de la distribución de la severidad (pérdidas por encima de un determinado umbral) pueden modelizarse usando una distribución Pareto Generalizada.

Se dice que la variable continua \(X\) tiene una distribución de Pareto con parámetro de forma \(\alpha\) y parámetro de escala \(\theta\) si su pdf viene dada por \[ f_{X}\left( x \right) = \frac{\alpha\theta^{\alpha}}{\left( x + \theta \right)^{\alpha + 1}} \ \ \ x > 0,\ \alpha > 0,\ \theta > 0. \] Los dos paneles de la Figura 3.2 muestran los efectos de los parámetros de escala y forma en la función de densidad Pareto.

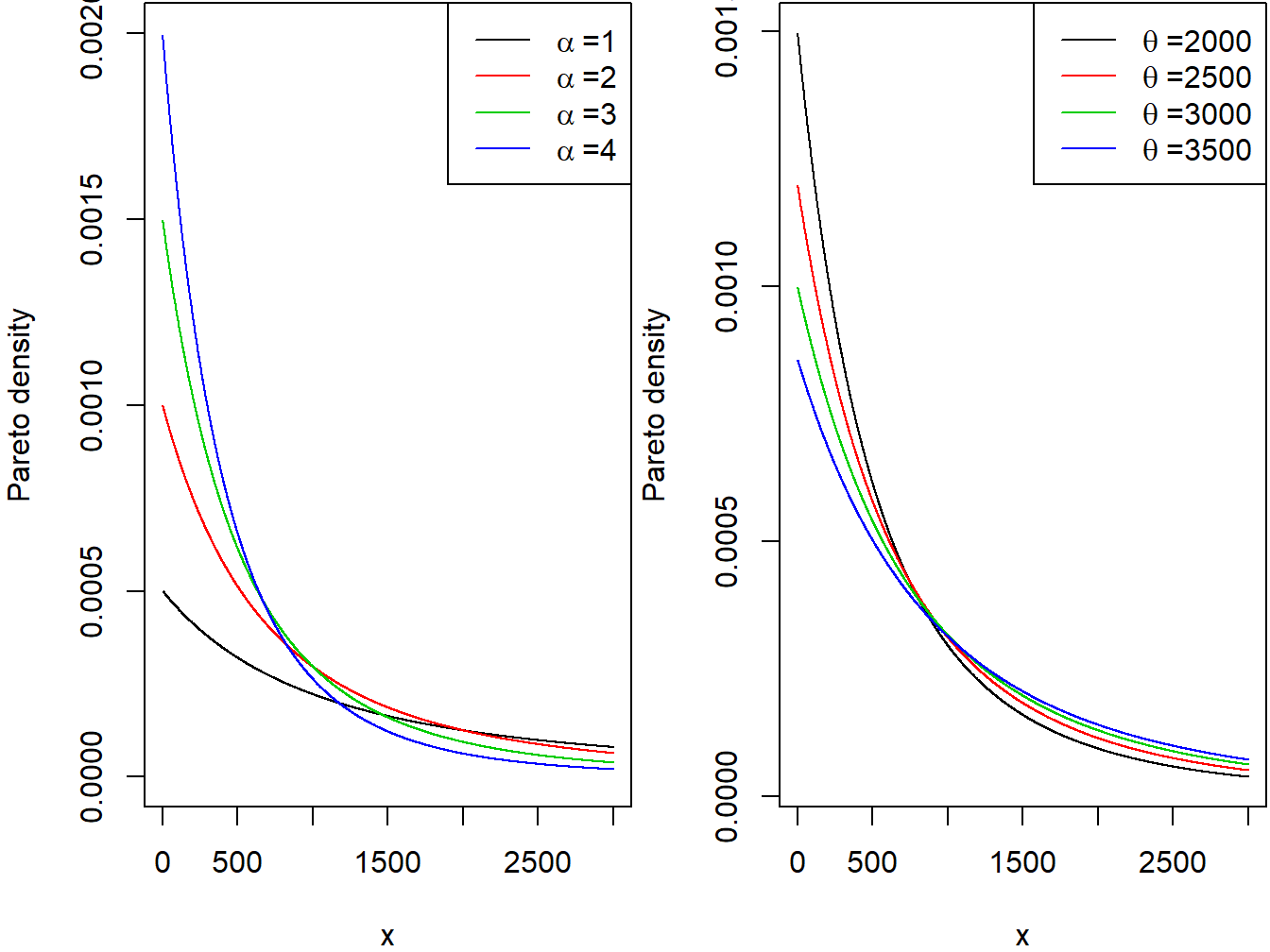
Figure 3.2: Densidades Pareto. El panel de la izquierda corresponde a escala=2000 y forma variable. El panel de la derecha corresponde a forma=3 y escala variable

Código R para los gráficos de la densidad Pareto

library(VGAM)

par(mfrow=c(1, 2), mar = c(4, 4, .1, .1))

# Densidades Pareto con forma variable
x <- seq(1, 3000, by = 1)
scaleparam <- seq(2000, 3500, 500)
shapeparam <- 1:4

# variando el parámetro de forma
plot(x, dparetoII(x, loc=0, shape = shapeparam[1], scale = 2000), ylim=c(0,0.002),type = "l", ylab = "Pareto density")
for(k in 2:length(shapeparam)){
  lines(x, dparetoII(x, loc=0, shape = shapeparam[k], scale = 2000), col = k)
}
legend("topright", c(expression(alpha~'=1'), expression(alpha~'=2'), expression(alpha~'=3'), expression(alpha~'=4')), lty=1, col = 1:4)

# Densidades de Pareto con escala variable
plot(x, dparetoII(x, loc=0, shape = 3, scale = scaleparam[1]), type = "l", ylab = "Pareto density")
for(k in 2:length(scaleparam)){
  lines(x, dparetoII(x, loc=0, shape = 3, scale = scaleparam[k]), col = k)
}
legend("topright", c(expression(theta~'=2000'), expression(theta~'=2500'), expression(theta~'=3000'), expression(theta~'=3500')), lty=1, col = 1:4)

La función de distribución de una Pareto viene dada por \[ F_{X}\left( x \right) = 1 - \left( \frac{\theta}{x + \theta} \right)^{\alpha} \ \ \ x > 0,\ \alpha > 0,\ \theta > 0. \] Se puede ver fácilmente que la función de riesgo de la distribución de Pareto es una función decreciente en \(x\), otro indicador de que es una distribución de cola pesada. Cuando la función de riesgo decrece con el tiempo la población fallece a una tasa decreciente dando como resultado una cola más pesada para la distribución. La función de riesgo revela información sobre la distribución de la cola y es frecuentemente usada para modelizar distribuciones en análisis de la supervivencia. La función de riesgo se define como la posibilidad instantánea de que el evento de interés ocurra dentro de un marco temporal muy pequeño.

El momento \(k\)-ésimo de una variable aleatoria con una distribución de Pareto existe si y solo si \(\alpha > k\). Si \(k\) es un entero positivo entonces \[ \mathrm{E}\left( X^{k} \right) = \frac{\theta^{k}~ k!}{\left( \alpha - 1 \right)\cdots\left( \alpha - k \right)} \ \ \ \alpha > k. \] La media y varianza vienen dadas por \[\mathrm{E}\left( X \right) = \frac{\theta}{\alpha - 1} \ \ \ \text{for } \alpha > 1\] y \[\mathrm{Var}\left( X \right) = \frac{\alpha\theta^{2}}{\left( \alpha - 1 \right)^{2}\left( \alpha - 2 \right)} \ \ \ \text{for } \alpha > 2,\]respectivamente.

Ejemplo 3.2.1. El tamaño de los siniestros en una cartera de asegurados sigue una distribución de Pareto con media y varianza iguales a 40 y 1800 respectivamente. Encuentra

1. Los parámetros de forma y escala.
2. El percentil 95 de la distribución.

Mostrar Solución de Ejemplo

Solución.

a. Dado que \(X\sim Pa(\alpha,\theta)\), se tiene que \(\mathrm{E}\left( X \right) = \frac{\theta}{\alpha - 1} = 40\) y \(\mathrm{Var}\left( X \right) = \frac{\alpha\theta^{2}}{\left( \alpha - 1 \right)^{2}\left( \alpha - 2 \right)} = 1800\). Dividiendo el cuadrado de la primera ecuación por la segunda obtenemos \(\frac{\alpha - 2}{\alpha} = \frac{40^{2}}{1800}\). Por tanto, \(\alpha = 18,02\) y \(\theta = 680,72\).
b. El percentil 95, \(\pi_{0,95}\), satisface la ecuación \[ F_{X}\left( \pi_{0,95} \right) = 1 - \left( \frac{680,72}{\pi_{0,95} + 680,72} \right)^{18,02} = 0,95. \] Por tanto, \(\pi_{0,95} = 122,96\).

---

3.2.3 Distribución Weibull

La distribución Weibull, denominada así por el físico sueco Waloddi Weibull (1887-1979) es ampliamente utilizada en fiabilidad, análisis de tiempos de vida, predicciones del tiempo y siniestros en seguros generales. Datos truncados aparecen frecuentemente en estudios de seguros. La distribución Weibull ha sido utilizada para modelizar el acuerdo de exceso de pérdida en el seguro del automóvil así como el tiempo entre la llegada de dos terremotos.

Se dice que la variable continua \(X\) sigue una distribución Weibull con parámetro de forma \(\alpha\) y parámetro de escala \(\theta\) si su función de densidad de probabilidad viene dada por \[ f_{X}\left( x \right) = \frac{\alpha}{\theta}\left( \frac{x}{\theta} \right)^{\alpha - 1} \exp \left(- \left( \frac{x}{\theta} \right)^{\alpha}\right) \ \ \ x > 0,\ \alpha > 0,\ \theta > 0. \] Los dos paneles de la Figura 3.3 muestran los efectos de los parámetros de escala y forma de la función de densidad de una Weibull.

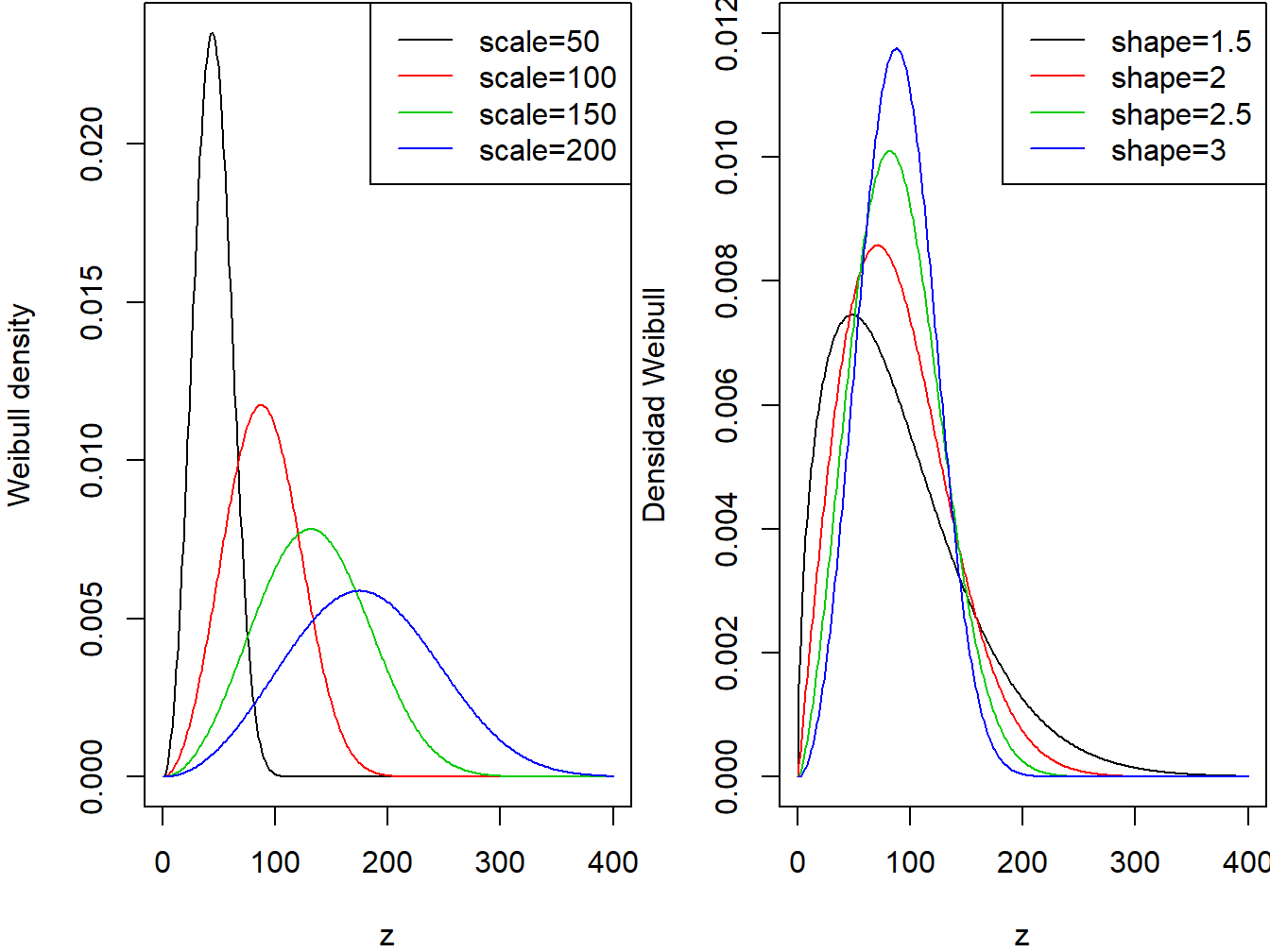
Figure 3.3: Densidades Weibull. El panel de la izquierda corresponde a forma=3 y escala variable. El panel de la derecha corresponde a escala=100 y forma variable.

Código R para los gráficos de la densidad Weibull

par(mfrow=c(1, 2), mar = c(4, 4, .1, .1))

# Densidad Weibull con escala variable
z<- seq(0,400,by=1)
scaleparam <- seq(50,200,50)
shapeparam <- seq(1.5,3,0.5)
plot(z, dweibull(z, shape = 3, scale = scaleparam[1]), type = "l", ylab = "Densidad Weibull")
for(k in 2:length(scaleparam)){
  lines(z,dweibull(z,shape = 3, scale = scaleparam[k]), col = k)}
legend("topright", c("scale=50", "scale=100", "scale=150", "scale=200"), lty=1, col = 1:4)

# Densidad Weibull con forma variable
plot(z, dweibull(z, shape = shapeparam[1], scale = 100), ylim=c(0,0.012), type = "l", ylab = "Densidad Weibull ")
for(k in 2:length(shapeparam)){
  lines(z,dweibull(z,shape = shapeparam[k], scale = 100), col = k)}
legend("topright", c("shape=1.5", "shape=2", "shape=2.5", "shape=3"), lty=1, col = 1:4)

La función de distribución de una Weibull viene dada por \[ F_{X}\left( x \right) = 1 - e^{- \left( x / \theta \right)^{\alpha}} \ \ \ x > 0,\ \alpha > 0,\ \theta > 0. \]

Se puede ver fácilmente que el parámetro de forma \(\alpha\) describe la forma de la función de riesgo de una distribución Weibull. La función de riesgo es una función decreciente cuando \(\alpha < 1\) (distribución de cola pesada), constante cuando \(\alpha = 1\) y creciente cuando \(\alpha > 1\) (distribución de cola ligera). Este comportamiento de la función de riesgo hace que la distribución de Weibull sea adecuada para una gran variedad de fenómenos como la predicción del tiempo, ingeniería eléctrica e industrial, modelización actuarial y análisis del riesgo financiero.

El momento \(k\)-ésimo de una variable aleatoria con distribución Weibull viene dado por \[ \mathrm{E}\left( X^{k} \right) = \theta^{k}~\Gamma\left( 1 + \frac{k}{\alpha} \right) . \]

La media y la varianza vienen dades por \[ \mathrm{E}\left( X \right) = \theta~\Gamma\left( 1 + \frac{1}{\alpha} \right) \] y \[ \mathrm{Var}(X)= \theta^{2}\left( \Gamma\left( 1 + \frac{2}{\alpha} \right) - \left\lbrack \Gamma\left( 1 + \frac{1}{\alpha} \right) \right\rbrack ^{2}\right), \] respectivamente.

Ejemplo 3.2.2. Se asume que la distribución de probabilidad del tiempo de vida de pacientes con SIDA (en meses) desde el momento del diagnóstico sigue una distribución de Weibull con parámetro de forma 1,2 y parámetro de escala 33,33.

1. Determina la probabilidad de que una persona de esta población elegida al azar sobreviva al menos 12 meses,
2. Se selecciona una muestra de 10 pacientes de esta población. Cuál es la probabilidad de que como máximo dos mueran al cabo de un año del diagnóstico.
3. Encuentra el percentil 99 de la distribución de los tiempos de vida.

Mostrar Solución de Ejemplo

Solución.

a. Sea \(X\) el tiempo de vida de los pacientes con SIDA (en meses) con distribución Weibull de parámetros \(\left(1,2,\ 33,33 \right)\). Tenemos,

\[ \Pr \left( X \geq 12 \right) = S_{X} \left( 12 \right) = e^{- \left( \frac{12}{33,33} \right)^{1,2}} = 0,746. \]

b. Sea \(Y\) el número de pacientes que mueren al cabo de un año del diagnóstico. Entonces, \(Y\sim Bin\left( 10,\ 0,254 \right)\) y \(\Pr\left( Y \leq 2 \right) = 0,514.\)

c. Sea \(\pi_{0,99}\) el percentil 99 de esta distribución. Entonces, \[ S_{X}\left( \pi_{0,99} \right) = \exp\left\{- \left( \frac{\pi_{0,99}}{33,33} \right)^{1,2}\right\} = 0,01. \] Resolviendo para \(\pi_{0,99}\), obtenemos \(\pi_{0,99} = 118,99\).

---

3.2.4 Distribución Beta Generalizada de segundo tipo

La Distribución Beta Generalizada de segundo tipo (GB2) fue introducida por Venter (1983) en el contexto de la modelización de las pérdidas en seguros y por McDonald (1984) como una distribución para los ingresos y la riqueza. Es una distribución de cuatro parámetros muy flexible que puede modelizar distribuciones con asimetria tanto positiva como negativa.

Se dice que la variable \(X\) tiene una distribución GB2 con parámetros \(\sigma\), \(\theta\), \(\alpha_1\) y \(\alpha_2\) si su función de densidad de probabilidad viene dada por

\[\begin{equation} f_{X}\left( x \right) = \frac{(x/\theta)^{\alpha_2/\sigma}}{x \sigma~\mathrm{B}\left( \alpha_1,\alpha_2\right)\left\lbrack 1 + \left( x/\theta \right)^{1/\sigma} \right\rbrack^{\alpha_1 + \alpha_2}} \ \ \ \text{for } x > 0, \tag{3.1} \end{equation}\]

\(\sigma,\theta,\alpha_1,\alpha_2 > 0\), y donde la función beta es \(\mathrm{B}\left( \alpha_1,\alpha_2 \right)\) definida como \[ \mathrm{B}\left( \alpha_1,\alpha_2\right) = \int_{0}^{1}{t^{\alpha_1 - 1}\left( 1 - t \right)^{\alpha_2 - 1}}~ dt. \]

La GB2 proporciona una modelo para datos con cola pesada así como ligera. Incluye a las distribuciones exponencial, gamma, Weibull, Burr, Lomax, F, chi-cuadrado, Rayleigh, lognormal y log-logistic como casos especiales o límite. Por ejemplo, estableciendo estos valores para los parámetros \(\sigma = \alpha_1 = \alpha_2 = 1\), la GB2 se reduce a la distribución log-logistic. Cuando \(\sigma = 1\) y \(\alpha_2 \rightarrow \infty\), se reduce a la distribución gamma y cuando \(\alpha = 1\) y \(\alpha_2 \rightarrow \infty\), se reduce a la distribución Weibull.

Una variable aleatoria GB2 puede ser definida como sigue. Se asume que \(G_1\) y \(G_2\) son variables aleatorias independientes donde \(G_i\) tiene una distribución gamma con parámetros \(\alpha_i\) y parámetro de escala igual a 1. Entonces, puede demostrarse que la variable aleatoria \(X = \theta \left(\frac{G_1}{G_2}\right)^{\sigma}\) sigue una distribución GB2 con pdf resumida en la ecuación (3.1). Este resultado teórico tiene diverses implicaciones. Por ejemplo, cuando los momentos existen, puede demostrarse que el momento \(k\)-ésimo de la variable aleatoria con distribución GB2 viene dado por \[ \mathrm{E}\left( X^{k} \right) = \frac{\theta^{k}~\mathrm{B}\left( \alpha_1 +k \sigma,\alpha_2 - k \sigma \right)}{\mathrm{B}\left( \alpha_1,\alpha_2 \right)}, \ \ \ k > 0. \]

Anteriormente la GB2 también había sido aplicada a datos de ingresos y más recientemente ha sido utilitzada para modelitzar datos de siniestros de cola larga (en la Sección 10.2 se describen diferentes interpretaciones del concepto “cola larga”). GB2 fue usada para modelizar diferentes tipos de siniestros en el seguro del automóvil, severidad de las pérdidas causades por el fuego así como datos de sinietros en seguros médicos.

3.3 Métodos para Crear Distribuciones Nuevas

---

En esta sección se mostrara como:

• Entender las conexiones entre distribuciones
• Proporcionar ideas sobre cuando una distribución es preferible en comparación con otras alternativas
• Proporcionar los fundamentos para la creación de nuevas distribuciones

---

3.3.1 Funciones de variables aleatorias y sus distribuciones

En la Sección 3.2 se han descrito algunas distribuciones fundamentales conocidas. En esta sección se describe la forma de crear nuevas distribuciones de probabilidad paramétricas a partir de otras existentes. Concretamente, sea \(X\) una variable aleatoria continua con función de densidad de probabilidad conocida \(f_{X}(x)\) y función de distribución \(F_{X}(x)\). Se desea conocer la distribución de \(Y = g\left( X \right)\), donde \(g(X)\) es una transformación uno-a-uno que define una nueva variable aleatoria \(Y\). Es esta sección se aplica las siguientes técnicas para crear nuevas familias de distribuciones: (a) multiplicación por una constante (b) elevación a una potencia, (c) exponenciación y (d) mixtura.

3.3.2 Multiplicación por una constante

Si los datos de siniestros muestran cambios a lo largo del tiempo entonces esta transformación puede ser útil para ajustar el efecto de la inflación. Si el nivel de la inflación es positivo entonces los costes de los siniestros están aumentando, y si es negativo los costes están decreciendo. Para realizar el ajuste por inflación multiplicamos el coste \(X\) por 1+ tasa de inflación (inflación negativa es deflacción). Para tener en cuenta el impacto de los tipos de cambio en los costes de los siniestros también usamos una transformación para aplicar la conversión de una moneda base a otra.

Se considera la transformación \(Y = cX\), donde \(c > 0\), entonces, la función de distribución de \(Y\) viene dada por \[ F_{Y}\left( y \right) = \Pr\left( Y \leq y \right) = \Pr\left( cX \leq y \right) = \Pr\left( X \leq \frac{y}{c} \right) = F_{X}\left( \frac{y}{c} \right). \] Por lo tanto, la función de densidad de probabilidad que se desea determinar \(f_{Y}(y)\) puede expresarse como \[ f_{Y}\left( y \right) = \frac{1}{c}f_{X}\left( \frac{y}{c} \right). \] Se asume que \(X\) pertenece a un cierto conjunto de distribuciones paramétricas y se define la versión reescalada \(Y\ = \ cX\), \(c\ > \ 0\). Si \(Y\) está en el mismo conjunto de distribuciones entonces se dice que la distribución es una distribución escala. Cuando un miembro de una distribución escala se multiplica por una constante \(c\) (\(c > 0\)), el parámetro de escala de esa distribución escala cumple dos condiciones:

1. El parámetro se transforma multiplicando por \(c\);
2. El resto de parámetros no se ven afectados.

Ejemplo 3.3.1. Pregunta de un examen actuarial. Las pérdidas agregadas de Eiffel Auto Insurance se denotan en Euros y siguen una distribución lognormal con \(\mu = 8\) y \(\sigma = 2\). Dado que 1 euro \(=\) 1,3 dólares, encuentra el conjunto de parámetros lognormales que describen la distribución de pérdidas de Eiffel en dólares.

Mostrar Solución de Ejemplo

Solución.

Sean \(X\) e \(Y\) las pérdidas agregadas de Eiffel Auto Insurance en euros y dólares respectivamente. Dado que \(Y = 1.3X\), tenemos, \[ F_{Y}\left( y \right) = \Pr\left( Y \leq y \right) = \Pr\left( 1.3X \leq y \right) = \Pr\left( X \leq \frac{y}{1,3} \right) = F_{X}\left( \frac{y}{1.3} \right). \]

\(X\) sigue una distribución lognormal con parámetros \(\mu = 8\) y \(\sigma = 2\). La función de densidad de probabilidad de \(X\) viene dada por \[ f_{X}\left( x \right) = \frac{1}{x \sigma \sqrt{2\pi}}\exp \left\{- \frac{1}{2}\left( \frac{\ln x - \mu}{\sigma} \right)^{2}\right\} \ \ \ \text{para } x > 0. \] Dado que \(\left| \frac{dx}{dy} \right| = \frac{1}{1,3}\), la función de densidad de probabilidad de interés \(f_{Y}(y)\) es \[ f_{Y}\left( y \right) = \frac{1}{1,3}f_{X}\left( \frac{y}{1,3} \right) \\ = \frac{1}{1,3}\frac{1,3}{y \sigma \sqrt{2\pi}}\exp \left\{- \frac{1}{2}\left( \frac{\ln\left( y/1.3 \right) - \mu}{\sigma} \right)^{2}\right\} \\ = \frac{1}{y \sigma\sqrt{2\pi}}\exp \left\{- \frac{1}{2}\left( \frac{\ln y - \left( \ln 1,3 + \mu \right)}{\sigma} \right)^{2}\right\}. \] Entonces \(Y\) sigue una distribución lognormal con parámetros \(\ln 1,3 + \mu = 8,26\) y \(\sigma = 2,00\). Si se establece que \(\mu = ln(m)\) entonces resulta fácil ver que \(m\)=\(e^{\mu}\) es el parámetro de escala que fue multiplicado por 1,3 mientras que \(\sigma\) es el parámetro de forma que no se ha visto alterado.

---

Ejemplo 3.3.2. Pregunta de un examen actuarial. Demuestra que la distribución gamma es una distribución escala.

Mostrar Solución de Ejemplo

Solución.

Sea \(X\sim Ga(\alpha,\theta)\) e \(Y = cX\). Dado que \(\left| \frac{dx}{dy} \right| = \frac{1}{c}\), entonces \[ f_{Y}\left( y \right) = \frac{1}{c}f_{X}\left( \frac{y}{c} \right) = \frac{\left( \frac{y}{c\theta} \right)^{\alpha}}{y~\Gamma\left( \alpha \right)}\exp \left( - \frac{y}{c\theta} \right) . \] Se puede ver que \(Y\sim Ga(\alpha,c\theta)\) lo cual indica que la gamma es una distribución escala y \(\theta\) es un parámetro de escala.

Usando el mismo enfoque podemos demostrar que otras distribuciones introducidas en la Sección 3.2 son también distribuciones escala. En la modelización actuarial, trabajar con una distribución escala es muy conveniente porque permite incorporar el efecto de la inflación y adaptar los cambios en la modeda correspondiente.

---

3.3.3 Elevación a una potencia

En la Sección 3.2.3 se ha tratado la fexibilidad de la distribución de Weibull para el ajuste de datos de fiabilidad. Teniendo en cuenta los orígenes de la distribución de Weibull, se reconoce que la Weibull es una transformación basada en la potencia de la distribución exponencial. Esta se una aplicación de otro tipo de transformación que implica elevar una variable aleatoria a una potencia.

Si se considera la transformación \(Y = X^{\tau}\), donde \(\tau > 0\), entonces la función de distribución de \(Y\) viene dada por \[ F_{Y}\left( y \right) = \Pr\left( Y \leq y \right) = \Pr\left( X^{\tau} \leq y \right) = \Pr\left( X \leq y^{1/ \tau} \right) = F_{X}\left( y^{1/ \tau} \right). \]

Por lo tanto, la función de densidad de probabilidad de interés \(f_{Y}(y)\) puede expresarse como \[ f_{Y}(y) = \frac{1}{\tau} y^{1/ \tau - 1} f_{X}\left( y^{1/ \tau} \right). \] Por otro lado, si \(\tau < 0\), la función de distribución de \(Y\) viene dada por \[ F_{Y}\left( y \right) = \Pr\left( Y \leq y \right) = \Pr\left( X^{\tau} \leq y \right) = \Pr\left( X \geq y^{1/ \tau} \right) = 1 - F_{X}\left( y^{1/ \tau} \right), \] y \[ f_{Y}(y) = \left| \frac{1}{\tau} \right|{y^{1/ \tau - 1}f}_{X}\left( y^{1/ \tau} \right). \]

Ejemplo 3.3.3. Se asume que \(X\) sigue una distribución exponencial con media \(\theta\) y se considera la variable transformada \(Y = X^{\tau}\). Demuestra que \(Y\) sigue una distribución de Weibull cuando \(\tau\) es positiva y determina los parámetros de la distribución de Weibull.

Mostrar Solución de Ejemplo

Solución.

Dado que \(X\) sigue una distribución exponencial con media \(\theta\), tenemos \[ f_{X}(x) = \frac{1}{\theta}e^{- x/ \theta} \ \ \ \, x > 0. \] Resolviendo para x se obtiene \(x = y^{1/\tau}\). Tomando derivadas, tenemos \[ \left| \frac{dx}{dy} \right| = \frac{1}{\tau}{y^{\frac{1}{\tau}-1}}. \] Así tenemos, \[ f_{Y}\left( y \right) = \frac{1}{\tau}{y^{\frac{1}{\tau} - 1}f}_{X}\left( y^{\frac{1}{\tau}} \right) \\ = \frac{1}{\tau \theta }y^{\frac{1}{\tau} - 1}e^{- \frac{y^{\frac{1}{\tau}}}{\theta}} = \frac{\alpha}{\beta}\left( \frac{y}{\beta} \right)^{\alpha - 1}e^{- \left( y/ \beta \right)^{\alpha}}. \] donde \(\alpha = \frac{1}{\tau}\) y \(\beta = \theta^{\tau}\). Entonces, \(Y\) sigue una distribución de Weibull con parámetro de forma \(\alpha\) y parámetro de escala \(\beta\).

---

3.3.4 Exponenciación

La distribución normal es un modelo muy popular para un gran número de aplicaciones y cuando el tamaño muestral es grande, puede servir como una distribucion aproximada para otros modelos. Si una variable aleatoria \(X\) tiene una distribución normal con media \(\mu\) y varianza \(\sigma^{2}\), entonces \(Y = e^{X}\) tiene una distribución lognormal con parámetros \(\mu\) y \(\sigma^{2}\). La variable aleatoria lognormal está acotada en cero por abajo, tiene asimetria positiva y tiene una larga cola por la derecha. La distribución lognormal es frecuentemente utilizada para describir la distribución de activos financieros como los precios de las acciones. También es usada para ajustar cuantías de siniestros en los seguros del automóvil y de salud. Este es un ejemplo de otro tipo de transformación que implica exponenciación.

En general, consideramos la transformación \(Y = e^{X}\). Entonces, la función de distribución de \(Y\) viene dada por \[F_{Y}\left( y \right) = \Pr\left( Y \leq y \right) = \Pr\left( e^{X} \leq y \right) = \Pr\left( X \leq \ln y \right) = F_{X}\left( \ln y \right).\] Tomando derivadas, vemos que la función de densidad de probabilidad de interés \(f_{Y}(y)\) puede expresarse como \[ f_{Y}(y) = \frac{1}{y}f_{X}\left( \ln y \right). \] Como un caso especial e importante, se asume que \(X\) tiene distribución normal con media \(\mu\) y varianza \(\sigma^2\). Entonces, la distribución de \(Y = e^X\) es

\[ f_{Y}(y) = \frac{1}{y}f_{X}\left( \ln y \right) = \frac{1}{y\sqrt{2 \pi}} \exp \left\{-\frac{1}{2}\left(\frac{ \ln y - \mu}{\sigma}\right)^2\right\}. \] A esta distribución se la conoce como la distribución lognormal.

Ejemplo 3.3.4. Pregunta de examen actuarial. Se asume que \(X\) tiene una distribución uniforme en el intervalo \((0,\ c)\) y definimos \(Y = e^{X}\). Determina la distribución de \(Y\).

Mostrar Solución de Ejemplo

Solución.

En primer lugar, se considera la cdf de \(Y\), \[ F_{Y}\left( y \right) = \Pr\left( Y \leq y \right) = \Pr\left( e^{X} \leq y \right) = \Pr\left( X \leq \ln y \right) = F_{X}\left( \ln y \right). \] Tomando derivadas, se tiene, \[ f_{Y}\left( y \right) = \frac{1}{y}f_{X}\left(\ln y \right) = \frac{1}{cy} . \] Dado que \(0 < x < c\), entonces \(1 < y < e^{c}\).

---

3.3.5 Mixturas finitas

Las distribuciones mixtas representan una forma útil de modelizar datos que provienen de una población heterogénea. Esta población de origen puede considerarse dividida en múltiples subpoblaciones con diferentes distribuciones.

3.3.5.1 Mixtura de dos variables

Si el fenómeno subyacente es diverso y puede ser ciertamente descrito como dos fenómenos que representan dos subpoblaciones con diferentes modelos, es posible construir la variable aleatoria de mixtura de dos variables \(X\). Sean las variables aleatorias \(X_{1}\) y \(X_{2}\), con funciones de densidad de probabilidad \(f_{X_{1}}\left( x \right)\) y \(f_{X_{2}}\left( x \right)\) respectivamente, la función de densidad de probabilidad de \(X\) es la media ponderada de la componente de la funcion de densidad de probabilidad \(f_{X_{1}}\left( x \right)\) y \(f_{X_{2}}\left( x \right)\). Las funciones de densidad de probabilidad y de distribución de \(X\) vienen dadas por \[f_{X}\left( x \right) = af_{X_{1}}\left( x \right) + \left( 1 - a \right)f_{X_{2}}\left( x \right),\] y \[F_{X}\left( x \right) = aF_{X_{1}}\left( x \right) + \left( 1 - a \right)F_{X_{2}}\left( x \right),\]

para \(0 < a <1\), donde los parámetros de mixtura \(a\) y \((1 - a)\) representan las proporciones de las observaciones de los datos que caen en cada una de las dos subpoblaciones repectivamente. Esta media ponderada puede ser aplicada a un buen número distribuciones relacionadas con cuantías. El momento k-ésimo y la función generatriz de momentos de \(X\) vienen dadas por \(\mathrm{E}\left( X^{k} \right) = a\mathrm{E}\left( X_{1}^{K} \right) + \left( 1 - a \right)\mathrm{E}\left( X_{2}^{k} \right)\), y \[M_{X}(t) = aM_{X_{1}}(t) + \left( 1 - a \right)M_{X_{2}}(t),\] respectivamente.

Ejemplo 3.3.5. Pregunta del examen actuarial. En un conjunto de pólizas de seguros se distinguen dos tipos. 25% de las pólizas son de Tipo 1 y 75% de Tipo 2. Para una póliza de Tipo 1, la cuantía de pérdida por año sigue una distribución exponencial con media 200, y para las pólizas de Tipo 2, la cuantía de perdidas por año sigue una distribución de Pareto con parámetros \(\alpha=3\) y \(\theta=200\). Para una póliza seleccionada al azar de la población total que incluye los dos tipos de pólizas, encuentra la probabilidad de que la pérdida anual sea inferior a 100, y determina la perdida media.

Mostrar Solución de Ejemplo

Solución.

Los dos tipos de pérdidas son las variables aleatorias \(X_1\) y \(X_2\). \(X_1\) digue una distribución exponencial con media 100, por lo tanto \(F_{X_1}\left(100\right)=1-e^{-\frac{100}{200}}=0,393\). \(X_2\) sigue una distribución de Pareto con parámetros \(\alpha=3\) y \(\theta=200\), por lo tanto \(F_{X_1}\left(100\right)=1-\left(\frac{200}{100+200}\right)^3=0,704\). Por lo tanto, \(F_X\left(100\right)=\left(0,25\times0,393\right)+\left(0,75\times0,704\right)=0,626\).

La pérdida media viene dada por \[\mathrm{E}\left(X\right)=0,25\mathrm{E}\left(X_1\right)+0,75\mathrm{E}\left(X_2\right)=\left(0,25\times200\right)+\left(0,75\times100\right)=125\].

---

3.3.5.2 Mixtura de k variables

En el caso de las distribuciones mixtas finitas, la variable aleatoria de interés \(X\) tiene una probabilidad \(p_{i}\) de provenir de una subpoblación homogénea \(i\), donde \(i = 1,2,\ldots,k\) y \(k\) es el número inicialment especificado de subpoblaciones en la mixtura. El parámetro de mixtura \(p_{i}\) representa la proporción de observaciones de la subpoblación \(i\). Se considera la variable aleatoria \(X\) que es generada por \(k\) subpoblaciones diferentes, donde la subpoblación \(i\) es modelizada con la distribución continua \(f_{X_{i}}\left( x \right)\). La distribución de probabilidad de \(X\) viene dada por \[f_{X}\left( x \right) = \sum_{i = 1}^{k}{p_{i}f_{X_{i}}\left( x \right)},\] donde \(0 < p_{i} < 1\) y \(\sum_{i = 1}^{k} p_{i} = 1\).

Este modelo es frecuentemente referenciado como mixtura finita o mixtura de \(k\) variables. La función de distribución, momento \(r\)-ésimo y funciones generatrices de momentos de la mixtura de \(k\) variables vienen dadas por

\[F_{X}\left( x \right) = \sum_{i = 1}^{k}{p_{i}F_{X_{i}}\left( x \right)},\] \[\mathrm{E}\left( X^{r} \right) = \sum_{i = 1}^{k}{p_{i}\mathrm{E}\left( X_{i}^{r} \right)}, \text{and}\] \[M_{X}(t) = \sum_{i = 1}^{k}{p_{i}M_{X_{i}}(t)},\] respectivamente.

Ejemplo 3.3.6. Pregunta de un examen actuarial. \(Y_{1}\) es una mixtura de \(X_{1}\) y \(X_{2}\) con ponderaciones de mixtura \(a\) y \((1 - a)\). \(Y_{2}\) es una mixtura de \(X_{3}\) y \(X_{4}\) con ponderaciones de mixtura \(b\) y \((1 - b)\). \(Z\) es una mixtura de \(Y_{1}\) y \(Y_{2}\) con ponderaciones de mixtura \(c\) y \((1 - c)\).

Demuestra que \(Z\) es una mixtura de \(X_{1}\), \(X_{2}\), \(X_{3}\) y \(X_{4}\), y determina las ponderaciones de mixtura.

Mostrar Solución de Ejemplo

Solución. Aplicando la fórmula para una distribución mixta, obtenemos \[f_{Y_{1}}\left( x \right) = af_{X_{1}}\left( x \right) + \left( 1 - a \right)f_{X_{2}}\left( x \right)\]

\[f_{Y_{2}}\left( x \right) = bf_{X_{3}}\left( x \right) + \left( 1 - b \right)f_{X_{4}}\left( x \right)\]

\[f_{Z}\left( x \right) = cf_{Y_{1}}\left( x \right) + \left( 1 - c \right)f_{Y_{2}}\left( x \right)\]

Sustituyendo las dos primeras ecuaciones en la tercera, obtenemos

\[f_{Z}\left( x \right) = c\left\lbrack af_{X_{1}}\left( x \right) + \left( 1 - a \right)f_{X_{2}}\left( x \right) \right\rbrack + \left( 1 - c \right)\left\lbrack bf_{X_{3}}\left( x \right) + \left( 1 - b \right)f_{X_{4}}\left( x \right) \right\rbrack\]

\[= caf_{X_{1}}\left( x \right) + c\left( 1 - a \right)f_{X_{2}}\left( x \right) + \left( 1 - c \right)bf_{X_{3}}\left( x \right) + (1 - c)\left( 1 - b \right)f_{X_{4}}\left( x \right)\].

Entonces, \(Z\) es una mixtura de \(X_{1}\), \(X_{2}\), \(X_{3}\) y \(X_{4}\), con pesos de mixtura \(\text{ca}\), \(c\left( 1 - a \right)\), \(\left( 1 - c \right)b\) y \((1 - c)\left( 1 - b \right)\), respectivamente. Se puede ver fácilmente que las ponderaciones de mixtura suman uno.

---

3.3.6 Mixturas continuas

Una mixtura con un gran número de subpoblaciones (\(k\) tiende a infinito) es frecuentemente denominada mixtura continua. En una mixtura continua, las subpoblaciones no se distinguen a través de un parámetro de mixtura discreto sino por una variable continua \(\Theta\), donde \(\Theta\) juega el papel de \(p_{i}\) en la mixtura finita. Se considera la variable aleatoria \(X\) con una distribución que depende de un parametro \(\Theta\), donde \(\Theta\) es a su vez una variable aleatoria continua. Esta descrición da lugar al siguiente modelo para \(X\) \[ f_{X}\left( x \right) = \int_{-\infty}^{\infty}{f_{X}\left(x \left| \theta \right. \right)g_{\Theta}( \theta )} d \theta , \] donde \(f_{X}\left( x | \theta \right)\) es la distribución condicional de \(X\) en un valor concreto de \(\Theta=\theta\) y \(g_{\Theta}\left( \theta \right)\) es la declaración realitzada sobre la probabilidad en relación con el parámetro \(\theta\) desconocido. En un contexto Bayesiano (descrito en la Sección 4.4), se le conoce como la distribución a priori de \(\Theta\) (la información a priori u opinión experta que se va a utilitzar en el análisis).

La función de distribución, momento \(k\)-ésimo y función generatriz de momentos de la mixtura continua vienen dadas por \[ F_{X}\left( x \right) = \int_{-\infty}^{\infty}{F_{X}\left(x \left| \theta \right. \right) g_{\Theta}(\theta)} d \theta, \] \[ \mathrm{E}\left( X^{k} \right) = \int_{-\infty}^{\infty}{\mathrm{E}\left( X^{k}\left| \theta \right. \right)g_{\Theta}(\theta)}d \theta, \] \[ M_{X}(t) = \mathrm{E}\left( e^{t X} \right) = \int_{-\infty}^{\infty}{\mathrm{E}\left( e^{ tx}\left| \theta \right. \right)g_{\Theta}(\theta)}d \theta, \] respectivamente.

El momento \(k\)-ésimo de la distribución mixta puede ser igualmente expresado como \[ \mathrm{E}\left( X^{k} \right) = \int_{-\infty}^{\infty}{\mathrm{E}\left( X^{k}\left| \theta \right. \right)g_{\Theta}(\theta)}d\theta ~=~ \mathrm{E}\left\lbrack \mathrm{E}\left( X^{k}\left| \Theta \right. \right) \right\rbrack . \]

Usando la ley de las esperanzas iteradas (ver Apéndice Capítulo 16), se puede definir la media y varianza de \(X\) como \[ \mathrm{E}\left( X \right) = \mathrm{E}\left\lbrack \mathrm{E}\left( X\left| \Theta \right. \right) \right\rbrack \] y \[ \mathrm{Var}\left( X \right) = \mathrm{E}\left\lbrack \mathrm{Var}\left( X\left| \Theta \right. \right) \right\rbrack + \mathrm{Var}\left\lbrack \mathrm{E}\left( X\left| \Theta \right. \right) \right\rbrack . \]

Ejemplo 3.3.7. Pregunta del examen actuarial. \(X\) tiene una distribución normal con media \(\Lambda\) y varianza 1. \(\Lambda\) tiene una distribución normal con media 1 y varianza 1. Determina la media y varianza de \(X\).

Mostrar Solución de Ejemplo

Solución.

X es una mixtura continua con media

\[ \mathrm{E}\left(X\right)=\mathrm{E}\left[\mathrm{E}\left(X\middle|\Lambda\right)\right]=\mathrm{E}\left(\Lambda\right)=1 \text{ and } \mathrm{V}\left(X\right)=\mathrm{V}\left[\mathrm{E}\left(X\middle|\Lambda\right)\right]+\mathrm{E}\left[\mathrm{V}\left(X\middle|\Lambda\right)\right]=\mathrm{V}\left(\Lambda\right)+\mathrm{E}\left(1\right)=1+1=2. \]

---

Ejemplo 3.3.8. Pregunta del examen actuarial. Las cuantías de los siniestros, \(X\), son uniformes en el intervalo \(\left(\Theta,\Theta+10\right)\) para cada asegurado. \(\Theta\) varía según el asegurado de acuerdo a una distribución exponencial con media 5. Determina la distribución incondicional, media y varianza de \(X\).

Mostrar Solución de Ejemplo

Solución.

La distribución condicional de \(X\) es \(f_{X}\left( \left. \ x \right|\theta \right) = \frac{1}{10}\) para \(\theta < x < \theta + 10\).

La distribución a priori de \(\theta\) es \(g_{\Theta}(\theta) = \frac{1}{5}e^{- \frac{\theta}{5}}\) para \(0 < \theta < \infty\).

La media y varianza condicionales de \(X\) vienen dadas por \[ \mathrm{E}\left( \left. \ X \right|\theta \right) = \frac{\theta + \theta + 10}{2} = \theta + 5 \] y \[ \mathrm{Var}\left( \left. \ X \right|\theta \right) = \frac{\left\lbrack \left( \theta + 10 \right) - \theta \right\rbrack^{2}}{12} = \frac{100}{12}, \] respectivamente.

Por lo tanto, la media y varianza incondicionales de \(X\) vienen dadas por

\[ \mathrm{E}\left( X \right) = \mathrm{E}\left\lbrack \mathrm{E}\left( X\left| \Theta \right. \right) \right\rbrack = \mathrm{E}\left( \Theta + 5 \right) = \mathrm{E}\left( \Theta \right) + 5 = 5 + 5 = 10, \]

y

\[ \mathrm{Var}\left( X \right) = \mathrm{E}\left\lbrack V\left( X\left| \Theta \right. \right) \right\rbrack + \mathrm{Var}\left\lbrack \mathrm{E}\left( X\left| \Theta \right. \right) \right\rbrack \\ = \mathrm{E}\left( \frac{100}{12} \right) + \mathrm{Var}\left( \Theta + 5 \right) = 8.33 + \mathrm{Var}\left( \Theta \right) = 33,33. \]

La distribucíon incondicional de \(X\) es

\[ f_{X}\left( x \right) = \int f_{X}\left( x |\theta \right) ~g_{\Theta}(\theta) d \theta . \]

\[ f_{X}\left( x \right) = \left\{ \begin{matrix} \int_{0}^{x}{\frac{1}{50}e^{- \frac{\theta}{5}}d\theta = \frac{1}{10}\left( 1 - e^{- \frac{x}{5}} \right)} & 0 \leq x \leq 10, \\ \int_{x - 10}^{x}{\frac{1}{50}e^{- \frac{\theta}{5}} d\theta} = \frac{1}{10}\left( e^{- \frac{\left( x - 10 \right)}{5}} - e^{- \frac{x}{5}} \right) & 10 < x < \infty. \\ \end{matrix} \right.\ \]

---

3.4 Modificaciones de Cobertura

En esta sección se evalúa el impacto de las modificaciones de cobertura: a) franquicias, b) límites en la póliza, c) coseguro e inflación en los costes del asegurador.

3.4.1 Franquicias

En una póliza con franquícia ordinaria, el asegurado (tomador) acepta cubrir una cantidad fija de un siniestro antes de que el asegurador comience a pagar. Este gasto fijo pagado de su bolsillo se llama franquícia y suele denotarse por \(d\). Si la cuantía del siniestro excede \(d\) entonces el asegurador es responsable de cubrir el coste X menos la franquicia \(d\). Dependiendo del acuerdo, la franquícia puede aplicarse a cada pérdida asegurada o al total de las pérdidas durante un determinado periodo (mes, año, etc.)

Las franquicias eliminan un gran número de pequeños siniestros, reduce el coste de gestionar y processar estos siniestros, reduce las primas para el tomador y reduce el riesgo moral. El riesgo moral ocurre cuando el asegurado asume más riesgos, aumentando las posibilidades de pérdidas debido a peligros frente a los que está asegurado, al saber que el asegurador se hará cargo de los costes (e.g. un asegurado con seguro frente a colisiones puede estar alentado a conducir temerariamente). Cuanto mayor sea la franquícia, el asegurado pagará primas más bajas por su póliza.

Sea \(X\) la pérdida incurrida para el asegurado e \(Y\) la cantidad del siniestro pagada por el asegurador. En relación con el beneficio pagado al tomador, se distinguen dos variables: el pago por pérdida y el pago por pago. La variable pago por pérdida, denotada por \(Y^{L}\) o \((X-d)_+\) está censurada por la izquierda porque los valores de \(X\) que son inferiores a \(d\) no son ignorados pero se igualan a cero. Esta variable incluye pérdidas para las que se realiza un pago así como pérdidas inferiores a la franquícia y por lo tanto se define como \[ Y^{L} = \left( X - d \right)_{+} = \left\{ \begin{array}{cc} 0 & X < d, \\ X - d & X > d \end{array} \right. . \] \(Y^{L}\) es frecuentemente denominada como una variable censurada por la izquierda y desplazada porque los valores por debajo de \(d\) no son ignorados y todas las pérdidas se ven desplazadas un valor \(d\).

Por otra parte, la variable pago por pago, denotada por \(Y^{P}\), está solo definida cuando existe un pago. Concretamente, \(Y^P\) es igual a \(X-d\) cuando \(\{X >d\}\), denotado como \(Y^P = X-d ||X>d\). Otra forma frecuentemente utilizada para expresarla es \[ Y^{P} = \left\{ \begin{matrix} \text{No definido} & X \le d \\ X - d & X > d \end{matrix} . \right. \] Por lo tanto, \(Y^{P}\) es frecuentemente referenciada como una variable truncada por la izquierda y desplazada o variable exceso de pérdida porque los siniestros inferiores a \(d\) no son reportados y los valores por encima de \(d\) se ven desplazados en \(d\) unidades.

Incluso cuando la distribución de \(X\) es continua, la distribución de \(Y^{L}\) es una combinación híbrida de una componente discreta y otra continua. La parte discreta de la distribución está concentrada en \(Y = 0\) (cuando \(X \leq d\)) y la parte continua se extiende sobre el intervalo \(Y > 0\) (cuando \(X > d\)). Para la parte discreta, la probabilidad de que no existan pagos es la probabiidad de que las pérdidas caigan por debajo de la franquícia; que es, \[\Pr\left( Y^{L} = 0 \right) = \Pr\left( X \leq d \right) = F_{X}\left( d \right).\] Usando la transformación \(Y^{L} = X - d\) para la parte continua de la distribución, se puede determinar la función de densidad de probabilidad de \(Y^{L}\) que viene dada por \[f_{Y^{L}}\left( y \right) = \left\{ \begin{matrix} F_{X}\left( d \right) & y = 0, \\ f_{X}\left( y + d \right) & y > 0 \end{matrix} \right. \]

Se puede ver que la variable pago por pago es la variable pago por pérdida condicionado a que la pérdida exceda la franquicia; es decir, \(Y^{P} = \left. \ Y^{L} \right|X > d\). Por lo tanto, la función de densidad de probabilidad de \(Y^{P}\) viene dada por \[f_{Y^{P}}\left( y \right) = \frac{f_{X}\left( y + d \right)}{1 - F_{X}\left( d \right)},\] para \(y > 0\). De acuerdo con esto, las funciones de distribución de \(Y^{L}\) y \(Y^{P}\) vienen dadas por \[F_{Y^{L}}\left( y \right) = \left\{ \begin{matrix} F_{X}\left( d \right) & y = 0, \\ F_{X}\left( y + d \right) & y > 0. \\ \end{matrix} \right.\ \] y \[F_{Y^{P}}\left( y \right) = \frac{F_{X}\left( y + d \right) - F_{X}\left( d \right)}{1 - F_{X}\left( d \right)},\] para \(y > 0\), respectivamente.

Los momentos ordinarios de \(Y^{L}\) y \(Y^{P}\) se pueden determinar directamente usando la función de densidad de probabilidad de \(X\) como sigue \[\mathrm{E}\left\lbrack \left( Y^{L} \right)^{k} \right\rbrack = \int_{d}^{\infty}\left( x - d \right)^{k}f_{X}\left( x \right)dx ,\] y \[ \mathrm{E}\left\lbrack \left( Y^{P} \right)^{k} \right\rbrack = \frac{\int_{d}^{\infty}\left( x - d \right)^{k}f_{X}\left( x \right) dx }{{1 - F}_{X}\left( d \right)} = \frac{\mathrm{E}\left\lbrack \left( Y^{L} \right)^{k} \right\rbrack}{{1 - F}_{X}\left( d \right)}, \] respectivamente. Para \(k=1\), se puede usar la función de supervivencia para calcular \(\mathrm{E}(Y^L)\) como \[ \mathrm{E}(Y^L) = \int_d^{\infty} [1-F_X(x)] ~dx . \] Esto puede ser facilmente demostrado si se considera la definición inicial de \(\mathrm{E}(Y^L)\) y se integra por partes.

Se ha visto que la franquicia \(d\) impuesta en una póliza de seguros es la cantidad de pérdida que ha de ser pagada del bolsillo del asegurado antes de que el asegurador realice ningún pago. La franquicia \(d\) impuesta en una póliza de seguros reduce la prima. La ratio de eliminación de pérdida (LER) es el porcentaje de decrecimiento en el pago esperado del asegurador como resultado de imponer una franquícia. LER se define como \[LER = \frac{\mathrm{E}\left( X \right) - \mathrm{E}\left( Y^{L} \right)}{\mathrm{E}\left( X \right)}.\]

Un tipo de franquícia no tan frecuente es la franquícia pura. La franquicia pura se aplica a la póliza de igual manera que la franquícia ordinaria excepto que cuando la pérdida excede la franquícia \(d\), la totalidad de la pérdida es cubierta por el asegurador. Las variables pago por pérdida y pago por pago en este caso se definen como \[Y^{L} = \left\{ \begin{matrix} 0 & X \leq d, \\ X & X > d, \\ \end{matrix} \right.\ \] y \[Y^{P} = \left\{ \begin{matrix} \text{No definido} & X \leq d, \\ X & X > d, \\ \end{matrix} \right.\ \] respectivamente.

Ejemplo 3.4.1. Pregunta del examen actuarial. Se asume que la distribución para la severidad de los siniestros es exponencial con media 1000. Una compañía de seguros pagará la cantidad de cada siniestro en exceso de una franquicia de 100. Calcula la varianza de la cantidad pagada por la compañía aseguradora por un siniestro, incluyendo la posibilidad de que la cantidad pagada sea 0.

Mostrar Solución de Ejemplo

Solution.

Sea \(Y^{L}\) la cantidad pagada por la compañía aseguradora por un siniestro. \[Y^{L} = \left( X - 100 \right)_{+} = \left\{ \begin{matrix} 0 & X \leq 100, \\ X - 100 & X > 100. \\ \end{matrix} \right.\ \] El primer y segundo momento de \(Y^{L}\) son \[E\left( Y^{L} \right) = \int_{100}^{\infty}\left( x - 100 \right)f_{X}\left( x \right)dx \\ = {\int_{100}^{\infty}{S_{X}\left( x \right)}dx = 1000e}^{- \frac{100}{1000}},\] y \[E\left\lbrack \left( Y^{L} \right)^{2} \right\rbrack = \int_{100}^{\infty}\left( x - 100 \right)^{2}f_{X}\left( x \right)dx \\\\ = 2 \times 1000^{2}e^{- \frac{100}{1000}}.\] Por lo tanto, \[\mathrm{Var}\left( Y^{L} \right) = \left( 2 \times 1000^{2}e^{- \frac{100}{1000}} \right) - \left( {1000e}^{- \frac{100}{1000}} \right)^{2} = 990,944.\]

Otra forma más simple para llegar a la solución consiste en usar la relación entre \(X\) e \(Y^{P}\). Si \(X\) tiene distribución exponencial con media 1000, entonces \(Y^{P}\) tiene también distribución exponencial con la misma media, debido a la propiedad de falta de memoria de la distribución exponencial. Por lo tanto, \(E\left( Y^{P} \right)\)=1000 y \[E\left\lbrack \left( Y^{P} \right)^{2} \right\rbrack = 2 \times 1000^{2}.\] Usando la relación entre \(Y^{L}\) y \(Y^{P}\) determinamos \[E\left( Y^{L} \right) = \ E\left( Y^{P} \right)S_{X}\left( 100 \right){= 1000e}^{- \frac{100}{1000}}\]

\[E\left\lbrack \left( Y^{L} \right)^{2} \right\rbrack = E\left\lbrack \left( Y^{P} \right)^{2} \right\rbrack S_{X}\left( 100 \right) = 2 \times 1000^{2}e^{- \frac{100}{1000}}.\]

La relación entre \(X\) e \(Y^P\) se puede usar también al trabajar con las distribuciones uniforme y Pareto. Puede demostrarse facilmente que si \(X\) es uniforme en el intervalo \(\left(0,\theta\right)\) entonces \(Y^P\) es uniforme en el intervalo \(\left(0,\theta-d\right)\) y si \(X\) es Pareto con parámetros \(\alpha\) y \(\theta\) entonces \(Y^P\) es Pareto con parámetros \(\alpha\) y \(\theta+d\).

---

Ejemplo 3.4.2. Pregunta del examen actuarial. Para un seguro:

• Las pérdidas tienen la función de densidad \[f_{X}\left( x \right) = \left\{ \begin{matrix} 0,02x & 0 < x < 10, \\ 0 & \text{en otros casos.} \\ \end{matrix} \right. \]
• El seguro tiene una franquicia ordinaria por pérdida de 4.
• \(Y^{P}\) es la variable aleatoria pago por pago.

Calcula \(\mathrm{E}\left( Y^{P} \right)\).

Mostrar Solución de Ejemplo

Solución.

Se define \(Y^P\) como sigue \[Y^{P} = \left\{ \begin{matrix} \text{Indefinido} & X \leq 4, \\ X - 4 & X > 4. \\ \end{matrix} \right.\ \] Por lo tanto, \(E\left( Y^{P} \right) = \frac{\int_{4}^{10}\left( x - 4 \right)0,02xdx}{{1 - F}_{X}\left( 4 \right)} = \frac{2,88}{0,84} = 3,43\).

Nótese que se divide por \(S_X(4)=1-F_X(4)\), dado que ese es el rango en el que la variable \(Y^P\) está definida.

---

Ejemplo 3.4.3. Pregunta del examen actuarial. Se proporcionan los siguientes datos:

1. Las pérdidas siguen una distribución exponencial con la misma media en todos los años. .
2. La ratio de eliminación de pérdida este año es 70%.
3. La franquicia ordinaria para el año siguiente es 4/3 de la franquicia actual.

Calcula la ratio de eliminación de pérdida para el siguiente año.

Mostrar Solución de Ejemplo

Solución.

Sean las pérdidas \(X\sim Exp(\theta)\) y la franquícia para el año próximo \(d' = \frac{4}{3}d\), la franquícia del año actual. La LER para el año actual es \[\frac{E\left( X \right) - E\left( Y^{L} \right)}{E\left( X \right)} = \frac{\theta - \theta e^{- d / \theta}}{\theta} = 1 - e^{- d / \theta} = 0,7.\] Entonces, \(e^{- d / \theta} = 0,3\).

La LER para el año próximo es \[\begin{align*} &\frac{\theta - \theta \exp(- \frac{d'}{\theta})}{\theta}=\frac{\theta - \theta \exp(- \frac{\left( \frac{4}{3}d \right)}{\theta})}{\theta} \\ &= 1 - \exp\left(- \frac{ \frac{4}{3} d }{\theta}\right) = 1 - \left( e^{-d /\theta} \right)^{4/3} = 1 - {0,3}^{4/3} = 0.8 . \end{align*}\]

---

3.4.2 Límites de la póliza

Cuando existe un límite en la póliza, el asegurador es responsable de cubrir la pérdida real \(X\) hasta el límite de cobertura. Este límite de cobertura fijado se llama límite de la póliza y se denota frecuentemente como \(u\). Si la pérdida excede el límite de la póliza, la diferencia \(X - u\) ha de ser pagada por el tomador. Mientras que un límite más alto para la póliza implica una compensación más alta para el asegurado, también se asocia a una prima mayor.

Sea \(X\) la pérdida incurrida por el asegurado e \(Y\) la cantidad pagada por el asegurador. La variable \(Y\) conocida como variable pérdida limitada se denota por \(X \land u\). Es una variable censurada por la derecha porque los valores por encima de \(u\) se igualan a \(u\). La variable aleatoria pérdida limitada \(Y\) se define como \[ Y = X \land u = \left\{ \begin{matrix} X & X \leq u, \\ u & X > u. \\ \end{matrix} \right.\ \] Se puede ver que la distinción entre \(Y^{L}\) e \(Y^{P}\) no es necesaria en el supuesto de una póliza limitada dado que el asegurador siempre hará un pago.

Usando las definiciones de \(\left(X-d\right)_+ \text{ y } \left(X\land d\right)\), se puede ver facilmente que el pago esperado sin modificaciones de cobertura, \(X\), es igual a la suma de los pagos esperados con una franquicia \(d\) y un límite \(d\). Es decir, \({X=\left(X-d\right)}_++ \left(X\land d\right)\).

Cuando una pérdida está sujeta a una franquicia \(d\) y un límite \(u\), la variable pago por pérdida \(Y^L\) se define como \[ Y^{L} = \left\{ \begin{matrix} 0 & X \leq d, \\ X - d & d < X \leq u, \\ u - d & X > u. \\ \end{matrix} \right.\ \] Por tanto, \(Y^L\) puede expresarse como \(Y^L=\left(X\land u\right)-\left(X\land d\right)\).

Aún cuando la distribución de \(X\) sea continua, la distribución de \(Y\) es una combinación híbrida de un componente discreto y uno continuo. La parte discreta de la distribución está concentrada en \(Y = u\) (cuando \(X > u\)), mientras que la parte continua se extiende en el intervalo \(Y < u\) (cuando \(X \leq u\)). Para la parte discreta, la probabilidad de que la compensación pagada sea \(u\), es la probabilidad de que la pérdida exceda el límite de la póliza \(u\); es decir, \[\Pr \left( Y = u \right) = \Pr \left( X > u \right) = {1 - F}_{X}\left( u \right).\] Para la parte continua de la distribución \(Y = X\), por lo tanto la función de densidad de probabilidad de \(Y\) viene dada por \[f_{Y}\left( y \right) = \left\{ \begin{matrix} f_{X}\left( y \right) & 0 < y < u, \\ 1 - F_{X}\left( u \right) & y = u. \\ \end{matrix} \right.\ \] De acuerdo con esto, la función de distribución de \(Y\) viene dada por \[F_{Y}\left( y \right) = \left\{ \begin{matrix} F_{X}\left( x \right) & 0 < y < u, \\ 1 & y \geq u. \\ \end{matrix} \right.\ \] Los momentos ordinarios de \(Y\) pueden determinarse directamente usando la función de densidad de probabilidad de \(X\) como sigue \[ \mathrm{E}\left( Y^{k} \right) = \mathrm{E}\left\lbrack \left( X \land u \right)^{k} \right\rbrack = \int_{0}^{u}x^{k}f_{X}\left( x \right)dx + \int_{u}^{\infty}{u^{k}f_{X}\left( x \right)} dx \\ = \int_{0}^{u}x^{k}f_{X}\left( x \right)dx + u^{k}\left\lbrack {1 - F}_{X}\left( u \right) \right\rbrack . \] For \(k=1\), we can use the survival function to calculate \(\mathrm{E}\left( Y \right)\) as follows \[ \mathrm{E}\left( Y \right) = \mathrm{E}\left( X \land u \right) = \int_{0}^{u} [1-F_{X}(x) ]dx . \] Esto puede ser demostrado facilmente si se considera la distribución inicial de \(\mathrm{E}\left( Y \right)\) y se hace una integración por partes.

Ejemplo 3.4.4. Pregunta del examen actuarial. A través de una póliza de seguro colectivo, un asegurador se compromete a pagar el 100% de las facturas médicas incurridas durante el año por los empleados de una pequeña compañía, hasta una cantidad total máxima de un millón de dólares. La cantidad total de facturas incurridas, \(X\), tiene función de densiad de probabilidad \[f_{X}\left( x \right) = \left\{ \begin{matrix} \frac{x\left( 4 - x \right)}{9} & 0 < x < 3, \\ 0 & \text{en otros casos.} \\ \end{matrix} \right.\ \] donde \(x\) se mide en millones. Calcula la cantidad total, en millones de dólares, que en términos esperados el asegurador pagará por esta póliza.

Mostrar Solución de Ejemplo

Solución.

Se define la cantidad total que el asegurador paga por las facturas como \[Y = X \land 1 = \left\{ \begin{matrix} X & X \leq 1, \\ 1 & X > 1. \\ \end{matrix} \right.\ \] Por lo tanto \(\mathrm{E}\left( Y \right) = \mathrm{E}\left( X \land 1 \right) = \int_{0}^{1}\frac{x^{2}(4 - x)}{9}dx + 1 * \int_{1}^{3}\frac{x\left( 4 - x \right)}{9}dx = 0,935\).

---

3.4.3 Coseguro e inflación

Tal y como hemos visto en la Sección 3.4.1 la cantidad de pérdida retenida por el tomador está limitada por el nivel de la franquicia \(d\). La pérdida retenida también puede ser un porcentaje del importe de los siniestros. El porcentaje \(\alpha\), a menudo denominado factor de coseguro, es el porcentaje del siniestro que la compañía ha de cubrir. Si la póliza está sujeta a una franquicia ordinaria y a un límite de la póliza, el coseguro se refiere al porcentaje del siniestro que el asegurador ha de cubrir, después de imponer la franquicia ordinaria y el límite de la póliza. La variable pago por pérdida, \(Y^{L}\), se define como \[ Y^{L} = \left\{ \begin{matrix} 0 & X \leq d, \\ \alpha\left( X - d \right) & d < X \leq u, \\ \alpha\left( u - d \right) & X > u. \\ \end{matrix} \right.\ \] El límite de la póliza (la cantidad máxima pagada por el asegurador) en este caso es \(\alpha\left( u - d \right)\), mientras que \(u\) es la pérdida máxima cubierta.

Hemos visto en la Sección 3.4.2 que cuando una pérdida está sujeta a una franquicia \(d\) y a un límite \(u\) la variable por pérdida \(Y^L\) puede expresarse como \(Y^L=\left(X\land u\right)-\left(X\land d\right)\). Con coseguro, se tiene que \(Y^L\) puede expresarse como \(Y^L=\alpha\left[(X\land u)-(X\land d)\right]\).

El momento \(k\)-ésimo de \(Y^{L}\) viene dado por \[ \mathrm{E}\left\lbrack \left( Y^{L} \right)^{k} \right\rbrack = \int_{d}^{u}\left\lbrack \alpha\left( x - d \right) \right\rbrack^{k}f_{X}\left( x \right)dx + \left\lbrack \alpha\left( u - d \right) \right\rbrack^{k} [1-F_{X}\left( u \right)] . \]

Un factor de incremento \(\left( 1 + r \right)\) se puede aplicar a \(X\) dando como resultado una variable aleatoria de pérdida ajustada por inflación \(\left( 1 + r \right)X\) (los valores de d y u preespecificados se mantienen inalterables). La variable por pérdida resultante se puede expresar como \[Y^{L} = \left\{ \begin{matrix} 0 & X \leq \frac{d}{1 + r}, \\ \alpha\left\lbrack \left( 1 + r \right)X - d \right\rbrack & \frac{d}{1 + r} < X \leq \frac{u}{1 + r}, \\ \alpha\left( u - d \right) & X > \frac{u}{1 + r}. \\ \end{matrix} \right.\ \] Los momentos primero y segundo de \(Y^{L}\) se pueden expresar como \[\mathrm{E}\left( Y^{L} \right) = \alpha\left( 1 + r \right)\left\lbrack \mathrm{E}\left( X \land \frac{u}{1 + r} \right) - \mathrm{E}\left( X \land \frac{d}{1 + r} \right) \right\rbrack,\] y \[\mathrm{E}\left\lbrack \left( Y^{L} \right)^{2} \right\rbrack = \alpha^{2}\left( 1 + r \right)^{2} \left\{ \mathrm{E}\left\lbrack \left( X \land \frac{u}{1 + r} \right)^{2} \right\rbrack - \mathrm{E}\left\lbrack \left( X \land \frac{d}{1 + r} \right)^{2} \right\rbrack \right. \\ \left. \ \ \ \ \ - 2\left( \frac{d}{1 + r} \right)\left\lbrack \mathrm{E}\left( X \land \frac{u}{1 + r} \right) - \mathrm{E}\left( X \land \frac{d}{1 + r} \right) \right\rbrack \right\} ,\] respectivamente.

Las fórmulas proporcionadas para los momentos primero y segundo de \(Y^{L}\) son generales. Bajo cobertura total, \(\alpha = 1\), \(r = 0\), \(u = \infty\), \(d = 0\) y \(\mathrm{E}\left( Y^{L} \right)\) se reduce a \(\mathrm{E}\left( X \right)\). Si solo se impone una franquicia ordinaria, \(\alpha = 1\), \(r = 0\), \(u = \infty\) y \(\mathrm{E}\left( Y^{L} \right)\) se reduce a \(\mathrm{E}\left( X \right) - \mathrm{E}\left( X \land d \right)\). Si solo se impone un límite en la póliza \(\alpha = 1\), \(r = 0\), \(d = 0\) y \(\mathrm{E}\left( Y^{L} \right)\) se reduce a \(\mathrm{E}\left( X \land u \right)\).

Ejemplo 3.4.5. Pregunta del examen actuarial. La variable aleatoria ground up loss para una póliza de seguro de salud en 2006 se modeliza con X, una distribución exponencial de media 1000. Una póliza de seguros paga las pérdidas por encima de una franquicia ordinaria de 100, con un máximo pago anual de 500. La variable aleatoria ground up loss se espera que sea 5% mayor en 2007, pero el seguro en 2007 tiene la misma franquícia y máximo pago como en 2006. Encuentra el porcentaje de incremento en el coste esperado por pago desde 2006 a 2007.

Mostrar Solución de Ejemplo

Solución.

Definimos la cantidad por pérdida \(Y^L\) en ambos años como \[Y_{2006}^{L} = \left\{ \begin{matrix} 0 & X \leq 100, \\ X - 100 & 100 < X \leq 600, \\ 500 & X > 600. \\ \end{matrix} \right.\ \]

\[Y_{2007}^{L} = \left\{ \begin{matrix} 0 & X \leq 95,24, \\ 1.05X - 100 & 95,24 < X \leq 571,43, \\ 500 & X > 571,43. \\ \end{matrix} \right.\ \]

Por lo tanto,

\[E\left( Y_{2006}^{L} \right) = E\left( X \land 600 \right) - E\left( X \land 100 \right) = 1000\left( {1 - e}^{- \frac{600}{1000}} \right) - 1000\left( {1 - e}^{- \frac{100}{1000}} \right)\]

\[= 356,026\].

\[E\left( Y_{2007}^{L} \right) = 1,05\left\lbrack E\left( X \land 571,43 \right) - E\left( X \land 95,24 \right) \right\rbrack\]

\[ = 1,05\left\lbrack 1000\left( {1 - e}^{- \frac{571,43}{1000}} \right) - 1000\left( {1 - e}^{- \frac{95,24}{1000}} \right) \right\rbrack \]

\[=361,659\].

\(E\left( Y_{2006}^{P} \right) = \frac{356,026}{e^{- \frac{100}{1000}}} = 393,469\).

\(E\left( Y_{2007}^{P} \right) = \frac{361,659}{e^{- \frac{95,24}{1000}}} = 397,797\).

Dado que \(\frac{E\left( Y_{2007}^{P} \right)}{E\left( Y_{2006}^{P} \right)} -1 = 0,011,\) hay un incremento del 1,1% desde 2006 a 2007. Debido al límite de la póliza, el coste por evento por pago creció solo un 1,1% entre 2006 y 2007 aunque las ground up losses aumentaron un 5% entre los dos años.

---

3.4.4 Reaseguro

En la Sección 3.4.1 se introdujo la franquicia en la póliza, que es un acuerdo contractual bajo el cual un asegurado transfiere parte del riesgo al asegurador que garantiza su cobertura a cambio del pago de una prima. En base a esta póliza, el asegurado ha de pagar todos los costes hasta el valor de la franquicia, y el asegurador solo paga la cantidad por encima de la franquicia (si la supera). Ahora se introduce el conceptoreaseguro, un mecanismo de seguro para las compañías aseguradoras. El reaseguro es un acuerdo contractual bajo el cual un asegurador transfiere la cobertura de parte de los riesgos subyacentes asegurados a otro asegurador (al que nos referimos como el reasegurador) a cambio de una prima de reaseguro. Aunque el reaseguro implica una relación entre tres partes: el asegurado original, el asegurador (a veces denominado cedente) y el reasegurador, el acuerdo de reaseguro solo implica al asegurador primario y al reasegurador. No existe relación contractual entre el asegurado original y el reasegurador. Aunque existen diferentes tipos de contratos de reaseguro, una forma común es la cobertura de exceso de pérdida. En estos contratos, el asegurador primario ha de hacer todos los pagos requeridos al asegurado hasta que el total de pagos del asegurador primario alcanza el valor de la franquicia fijada en el reaseguro. El reasegurador es entonces solo responsable del pago de cuantías por encima de la franquícia de reaseguro. La cantidad máxima retenida por el asegurador primario en el acuerdo de reaseguro (la franquícia de reaseguro) se denomina retención.

Los acuerdos de reaseguro permiten a los aseguradores con recursos financieros limitados incrementar su capacidad de suscribir pólizas y cumplir con los requerimientos realizados por los clientes para cobertures de seguro mayores al tiempo que reducen el impacto de pérdidas potenciales y protegen la compañía aseguradora frente a pérdidas castastróficas. El reasseguro también permite al asegurador primario beneficiarse de las habilidades de suscripción, la experiencia y la gestión compleja y competente de los archivos de reclamaciones de las compañías de reaseguro más grandes.

Ejemplo 3.4.6. Pregunta del examen actuarial. Las pérdidas que se derivan de una determinada cartera tienen una distribución de Pareto de dos parámetros con \(\alpha=5\) y \(\theta=3.600\). Se ha firmado un acuerdo de reaseguro, bajo el cual (a) el reasegurador acepta un 15% de las pérdidas hasta \(u=5.000\) y todas las cantidades en exceso de 5.000 y (b) el asegurador paga el resto de pérdidas.

1. Expresa las variables aleatorias para los pagos del reasegurador y asegurador en función de \(X\), las pérdidas de la cartera.
2. Calcula la cantidad media pagada por el asegurador por un único siniestro.
3. Asumiendo que el límite superior es \(u = \infty\), calcula un límite superior para la desviación estándar de la cantidad pagada por un único siniestro por el asegurador (reteniendo el 15% de copago).

Mostrar Solución de Ejemplo

Solución.

1. La porción del reasegurador es

\[ Y_{reasegurador} = \left\{ \begin{array}{cc} 0,15 X & X < 5000, \\ 0,15(5000) + X-5000 & X \ge 5000 \end{array} \right. . \]

Y la porción del asegurador es

\[ Y_{asegurador} = \left\{ \begin{array}{cc} 0,85 X & X < 5000, \\ 0,85(5000) & X \ge 5000 \end{array} \right. = 0,85(X \wedge 5000). \] b) Usando las tablas para el valor esperado limitado de una distribución de Pareto, tenemos

\[ \mathrm{E}~Y_{asegurador} = 0,85~\mathrm{E}~(X \wedge 5000)= 0,85~\frac{\theta}{\alpha-1}\left[ 1- \left(\frac{\theta}{5000+\theta}\right)^{\alpha-1} \right] \\ = 0,85~\frac{3600}{5-1}\left[ 1- \left(\frac{3600}{5000+3600}\right)^{5-1}\right] = 741,5103. \] c) Para el primer momento de la variable no limitada, tenemos

\[ \mathrm{E}~Y_{asegurador}(u=\infty) = 0,85~\mathrm{E}~X = 0,85~\frac{\theta}{\alpha-1} = 0,85~\frac{3600}{5-1} = 765. \] Para el segundo momento de la variable no limitada, usamos la tabla de distribuciones para obtener

\[ \mathrm{E}~Y_{asegurador}(u=\infty)^2 = 0,85^2~\mathrm{E}~X^2 = 0,85^2~\frac{\theta^2 \Gamma(2+1)\Gamma(\alpha-2)}{\Gamma(\alpha)} \\ = 0,85^2~\frac{3600^2 *2*2}{24} = 1560600. \] Por tanto, la varianza es \(1560600-765^2 =975375.\) Alternativamente, se puede usar la fórmula

\[ 0,85^2~\mathrm{Var}~X = 0,85^2~\frac{\alpha \theta^2}{(\alpha-1)^2(\alpha-2)} \\ = 0,85^2~\frac{5(3600^2)}{(5-1)^2(5-2)} = 975375. \]

Tomando raíces cuadradas, la desviación estándar es \(\sqrt{975375} \approx 987,6108\).

---

En la Sección 3.4.4 se proporcionaran más detalles sobre el reaseguro.

3.5 Estimación por Máxima Verosimilitud

---

En esta sección, se describirá cómo:

• Definir la verosimilitud para una muestra de observaciones de una distribución continua
• Definir el estimador de máxima verosimilitud para una muestra aleatoria de observaciones de una distribución continua
• Estimar distribuciones paramétricas basándose en datos agrupados, censurados y truncados

---

3.5.1 Estimadores de máxima verosimilitud para datos completos

Hasta este punto, este capítulo se ha centrado en distribuciones paramétricas que son frecuentemente usadas en aplicacions en el mundo asegurador. No obstante, para ser útiles en el trabajo aplicado, estas distribuciones deben usar valores “realistas” para los parámetros, y para ello es necesario volver a los datos. Fundamentalmente, asumimos que el analista dispone de una muestra aleatoria \(X_1, \ldots, X_n\) de una distribución con función de distribución \(F_X\) (por simplicidad, a veces se omite el subíndice \(X\)). Como es común, se usa el vector \(\boldsymbol \theta\) para denotar el conjunto de parámetros de \(F\). Este esquema básico de la muestra es revisado en la Sección Appendix 15.1. Aunque sea básico, este esquema de muestreo proporciona los fundamentos para entender esquemas más complejos que son regularmente usados en la práctica, y por lo tanto es importante dominar los conceptos básicos.

Antes de obtener valores aleatorios de una distribución, se consideran los resultados potenciales resumidos por una variable aleatoria \(X_i\) (aquí, \(i\) es 1, 2, …, \(n\)). Después de obtener el valor aleatorio, se observa \(x_i\). En relación con la notación, se usa letras romanas mayúsculas para variables aleatorias y minúscules para las realizaciones. Ya se ha presentado este planteamiento en la Sección 2.4, donde se ha usado \(\Pr(X_1 =x_1, \ldots, X_n=x_n)\) para cuantificar la “verosimilitud” de extraer una muestra \(\{x_1, \ldots, x_n\}\). Con datos continuos, se usa la función de densidad de probabilidad conjunta (pdf) en lugar de probabilidades conjuntas. Asumiendo independencia, la pdf conjunta puede ser expressada como el producto de pdfs. Por lo tanto, se define la verosimilitud como

\[\begin{equation} L(\boldsymbol \theta) = \prod_{i=1}^n f(x_i) . \tag{3.2} CREO QUE ESTO ES UN LABEL Y DE DEBERIA SALIR \end{equation}\]

A partir de esta notación, es necesario destacar que se considera esta función una función de los parámetros en \(\boldsymbol \theta\), con los datos \(\{x_1, \ldots, x_n\}\) fijos. El estimador de máxima verosimilitud es aquel valor de los parámetros en \(\boldsymbol \theta\) que maximiza \(L(\boldsymbol \theta)\).

De cálculo, se sabe que maximizar una función produce el mismo resultado que maximizar el logaritmo de la función (esto es debido a que el logaritmo es una función monótona convexa). Dado que obtenemos los mismos resultados, para facilitar las consideraciones computacionales, es común considerar la verosimilitud logarítmica, denotada como

\[\begin{equation} l(\boldsymbol \theta) = \ln L(\boldsymbol \theta) = \sum_{i=1}^n \ln f(x_i) . (\#eq:Verosimilitud logarítmica) \end{equation}\]

Ejemplo 3.5.1. Pregunta del examen actuarial. Se proporcionan las siguientes cinco observaciones: 521, 658, 702, 819, 1217. Se usa una Pareto de un único parámetro con función de distribución: \[ F(x) = 1- \left(\frac{500}{x}\right)^{\alpha}, ~~~~ x>500 . \]

Con \(n=5\), el logaritmo de la función de verosimilitud es \[ l(\alpha|\mathbf{x} ) = \sum_{i=1}^5 \ln f(x_i;\alpha ) = 5 \alpha \ln 500 + 5 \ln \alpha -(\alpha+1) \sum_{i=1}^5 \ln x_i. \] La Figura 3.4 muestra la verosimilitud logarítmica como función del parámetro \(\alpha\).

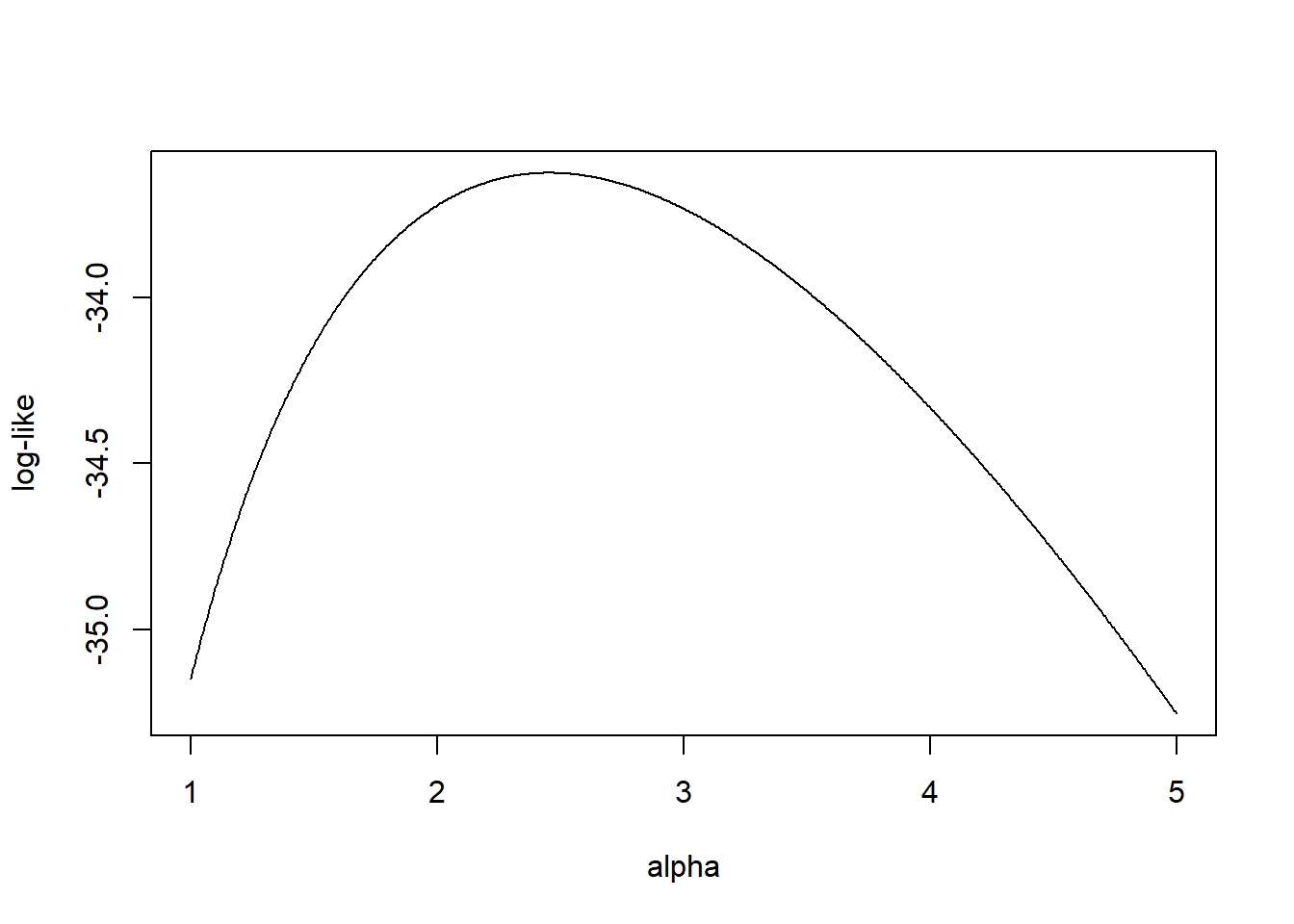
Figure 3.4: Verosimilitud logarítmica para una Pareto de un parámetro

Se puede determinar el valor máximo del logaritmo de la verosimilitud tomando derivadas e igualándolas a cero. De esto resulta \[ \frac{ \partial}{\partial \alpha } l(\alpha |\mathbf{x}) = 5 \ln 500 + 5 / \alpha - \sum_{i=1}^5 \ln x_i =_{set} 0 \Rightarrow \hat{\alpha}_{MLE} = \frac{5}{\sum_{i=1}^5 \ln x_i - 5 \ln 500 } = 2,453 . \]

Naturalmente, hay muchos problemas en los que no es práctico realizar un cálculo manual para la optimización. Afortunadamente hay muchas rutinas estadísticas disponibles como la función optim de R.

Código de R para la optimización

c1 <- log(521)+log(658)+log(702)+log(819)+log(1217)
nloglike <- function(alpha){-(5*alpha*log(500)+5*log(alpha)-(alpha+1)*c1)}
MLE <- optim(par=1, fn=nloglike)$par

---

Este código confirma el resultado del cálculo manual en el que el estimador máximo verosímil es \(\alpha_{MLE} =\) 2.453125.

---

Se presentan algunos ejemplos adicionales para ilustrar cómo los actuarios ajustan modelos de distribución paramétricos a una base de datos de siniestros usando máxima verosimilitud.

Ejemmplo 3.5.2. Pregunta de examen actuarial. Se considera una muestra aleatoria de cuantías de siniestros: 8.000 10.000 12.000 15.000. Se asume que la cuantía de los siniestros sigue una distribución inversa exponencial, con parámetro \(\theta\). Calcula el estimador máximo verosímil de \(\theta\).

Mostrar Solución de Ejemplo

Solución.

La función de densidad de probabilidad es \[f_{X}\left( x \right) = \frac{\theta e^{- \frac{\theta}{x}}}{x^{2}}, \] donde \(x > 0\).

La función de verosimilitud, \(L\left( \theta \right)\), puede ser vista como la probabilidad de los datos observados, expresada en función de los parámetros del modelo \(\theta\) \[L\left( \theta \right) = \prod_{i = 1}^{4}{f_{X_{i}}\left( x_{i} \right)} = \frac{\theta^{4}e^{- \theta\sum_{i = 1}^{4}\frac{1}{x_{i}}}}{\prod_{i = 1}^{4}x_{i}^{2}}.\]

El logaritmo de la función de verosimilitud, \(\ln L \left( \theta \right)\), es la suma de los logarítmos individuales. \[\ln L \left( \theta \right) = 4 \ln \theta - \theta\sum_{i = 1}^{4}\frac{1}{x_{i}} - 2\sum_{i = 1}^{4}\ln x_{i} .\]

\[ \frac{d \ln L \left( \theta \right)}{d \theta} = \frac{4}{\theta} - \sum_{i = 1}^{4}\frac{1}{x_{i}}. \]

El estimador máximo verosímil de \(\theta\), denotado como \(\hat{\theta}\), es la solución para la ecuación \[\frac{4}{\hat{\theta}} - \sum_{i = 1}^{4}{\frac{1}{x_{i}} = 0}.\] Por tanto, \(\hat{\theta} = \frac{4}{\sum_{i = 1}^{4}\frac{1}{x_{i}}} = 10.667\)

La segunda derivada de \(\ln L \left( \theta \right)\) viene dada por \[\frac{d^{2}\ln L\left( \theta \right)}{d\theta^{2}} = \frac{- 4}{\theta^{2}}.\] Evaluando la segunda derivada del logaritmo de la función de verosimilitud en \(\hat{\theta} = 10.667\) da un valor negativo, lo cual indica que \(\hat{\theta}\) es el valor que maximiza el logaritmo de la función de verosimilitud.

---

Ejemplo 3.5.3. Pregunta del examen actuarial. Una muestra aleatoria de tamaño 6 proviene de una distribución lognormal con parámetros \(\mu\) y \(\sigma\). Los valores de la muestra son 200, 3.000, 8.000, 60.000, 60.000, 160.000. Calcula el estimador máximo verosímil de \(\mu\) y \(\sigma\).

Mostrar Solución de Ejemplo

Solución.

La función de densidad de probabilidad es \[f_{X}\left( x \right) = \frac{1}{x \sigma \sqrt{2\pi}}\exp - \frac{1}{2}\left( \frac{\ln x - \mu}{\sigma} \right)^{2},\] donde \(x > 0\).

La función de verosimilitud, \(L\left( \mu,\sigma \right)\), es el producto de la pdf para cada punto. \[L\left( \mu,\sigma \right) = \prod_{i = 1}^{6}{f_{X_{i}}\left( x_{i} \right)} = \frac{1}{\sigma^{6}\left( 2\pi \right)^{3}\prod_{i = 1}^{6}x_{i}}exp - \frac{1}{2}\sum_{i = 1}^{6}\left( \frac{\ln x_{i} - \mu}{\sigma} \right)^{2}.\] El logaritmo de la función de verosimilitud, \(\ln L \left( \mu,\sigma \right)\), es la suma de los logaritmos individuales. \[\ln \left( \mu,\sigma \right) = - 6 \ln \sigma - 3 \ln \left( 2\pi \right) - \sum_{i = 1}^{6}\ln x_{i} - \frac{1}{2}\sum_{i = 1}^{6}\left( \frac{\ln x_{i} - \mu}{\sigma} \right)^{2}.\] Las primeras derivadas parciales son \[\frac{\partial \ln L\left( \mu,\sigma \right)}{\partial\mu} = \frac{1}{\sigma^{2}}\sum_{i = 1}^{6}\left( \ln x_{i} - \mu \right).\] \[\frac{\partial \ln L\left( \mu,\sigma \right)}{\partial\sigma} = \frac{- 6}{\sigma} + \frac{1}{\sigma^{3}}\sum_{i = 1}^{6}\left( \ln x_{i} - \mu \right)^{2}.\] Los estimadores máximo verosímiles de \(\mu\) y \(\sigma\), denotados como \(\hat{\mu}\) y \(\hat{\sigma}\), son las soluciones de las ecuaciones \[\frac{1}{{\hat{\sigma}}^{2}}\sum_{i = 1}^{6}\left( \ln x_{i} - \hat{\mu} \right) = 0.\] \[\frac{- 6}{\hat{\sigma}} + \frac{1}{{\hat{\sigma}}^{3}}\sum_{i = 1}^{6}\left( \ln x_{i} - \hat{\mu} \right)^{2} = 0.\] Esto resulta en las estimaciones

\[\hat{\mu} = \frac{\sum_{i = 1}^{6}{\ln x_{i}}}{6} = 9,38 \ \ \ \text{y} \ \ \ {\hat{\sigma}}^{2} = \frac{\sum_{i = 1}^{6}\left( \ln x_{i} - \hat{\mu} \right)^{2}}{6} = 5,12 . \].

Las segundas derivadas parciales son

\[ \frac{\partial^{2}\ln L\left( \mu,\sigma \right)}{\partial\mu^{2}} = \frac{- 6}{\sigma^{2}}, \ \ \ \ \frac{\partial^{2}\ln L\left( \mu,\sigma \right)}{\partial\mu\partial\sigma} = \frac{- 2}{\sigma^{3}}\sum_{i = 1}^{6}\left( \ln x_{i} - \mu \right) \]

y

\[ \frac{\partial^{2}\ln L\left( \mu,\sigma \right)}{\partial\sigma^{2}} = \frac{6}{\sigma^{2}} - \frac{3}{\sigma^{4}}\sum_{i = 1}^{6}\left( \ln x_{i} - \mu \right)^{2} \].

---

Dos cuestiones que vendrían a continuación tienen que ver con las propiedades para muestras grandes que el lector puede haber visto en cursos anteriores. El Capítulo del Apéndice 17 revisa la definición de función de verosimilitud, introduce sus propiedades, revisa los estimadores máximo verosímiles, extiende sus propiedades para muestras grandes al caso en el que hay múltiples parámetros en el modelo, y revisa la inferencia estadística basada en los estimadores máximo verosímiles. En las soluciones de estos ejemplos se derivan las varianzas asintóticas de los estimadores máximo verosímiles de los parámetros del modelo. Se usa el método delta para derivar las varianzas asintóticas de las funciones de estos parámetros.

Ejemplo 3.5.2 - Continuación. Se refiere al Ejemplo 3.5.2.

1. Aproxima la varianza del estimador máximo verosímil.
2. Determina un intervalo de confianza para \(\theta\) al 95%.
3. Determina un intervalo de confianza del 95% para \(\Pr \left( X \leq 9.000 \right).\)

Mostrar Solución de Ejemplo

Solución.

a. Tomando el recíproco de la esperanza negativa de la segunda derivada de \(\ln L \left( \theta \right)\), se obtiene una estimación de la varianza de \(\hat{\theta}\), \(\widehat{Var}\left( \hat{\theta} \right) = \left. \ \left\lbrack E\left( \frac{d^{2}\ln L \left( \theta \right)}{d\theta^{2}} \right) \right\rbrack^{- 1} \right|_{\theta = \hat{\theta}} = \frac{{\hat{\theta}}^{2}}{4} = 28.446.222\).

Nótese que dado que el tamaño de la muestra \(n \rightarrow \infty\), la distribución del estimador máximo verosímil \(\hat{\theta}\) converge a una distribución normal con media \(\theta\) y varianza \(\hat{V}\left( \hat{\theta} \right)\). El intervalo de confianza aproximado en este ejemplo se basa en el supuesto de normalidad, a pesar del pequeño tamaño muestral, solo con fines ilustrativos.

b. El intervalo de confianza al 95% para \(\theta\) viene dado por

\[ 10.667 \pm 1,96\sqrt{28.446.222} = \left( 213,34,\ 21.120,66 \right). \]

c. La función de distribución de \(X\) es \(F\left( x \right) = 1 - e^{- \frac{x}{\theta}}\). Entonces, el estimador máximo verosímil de \(g_{\Theta}(\theta) = F\left( 9.000 \right)\) es \[g\left( \hat{\theta} \right) = 1 - e^{- \frac{9.000}{10.667}} = 0,57.\] Se usa el método delta para aproximar la varianza de \(g\left( \hat{\theta} \right)\). \[\frac{\text{dg}\left( \theta \right)}{d \theta} = {- \frac{9.000}{\theta^{2}}e}^{- \frac{9.000}{\theta}}.\]

\(\widehat{Var}\left\lbrack g\left( \hat{\theta} \right) \right\rbrack = \left( - {\frac{9.000}{{\hat{\theta}}^{2}}e}^{- \frac{9.000}{\hat{\theta}}} \right)^{2}\hat{V}\left( \hat{\theta} \right) = 0,0329\).

El intervalo de confianza al 95% para \(F\left( 9.000 \right)\) viene dado por \[0,57 \pm 1,96\sqrt{0,0329} = \left( 0,214,\ 0,926 \right).\]

---

Ejemplo 3.5.3 - Continuación. Se refiere al Ejemplo 3.5.3.

1. Estima la matriz de covarianzas del estimador máximo verosímil.
2. Determina intervalos de confianza aproximados al 95% para \(\mu\) y \(\sigma\).
3. Determina un intervalo de confianza aproximado al 95% para la media de la distribución lognormal.

Mostrar Solución de Ejemplo

a. Para obtener la matriz de covarianzas del mle es necesario encontrar esperanzas de las segundas derivadas. Dado que la variable aleatoria \(X\) sigue una distribución lognormal con parámetros \(\mu\) y \(\sigma\), entonces \(\text{lnX}\) se distribuye como una normal con media \(\mu\) y varianza \(\sigma^{2}\).

\(\mathrm{E}\left( \frac{\partial^{2}\text{lnL}\left( \mu,\sigma \right)}{\partial\mu^{2}} \right) = \mathrm{E}\left( \frac{- 6}{\sigma^{2}} \right) = \frac{- 6}{\sigma^{2}}\),

\(\mathrm{E}\left( \frac{\partial^{2}\text{lnL}\left( \mu,\sigma \right)}{\partial\mu\partial\sigma} \right) = \frac{- 2}{\sigma^{3}}\sum_{i = 1}^{6}{\mathrm{E}\left( \ln x_{i} - \mu \right)} = \frac{- 2}{\sigma^{3}}\sum_{i = 1}^{6}\left\lbrack \mathrm{E}\left( \ln x_{i} \right) - \mu \right\rbrack\)=\(\frac{- 2}{\sigma^{3}}\sum_{i = 1}^{6}\left( \mu - \mu \right) = 0\),

y

\(\mathrm{E}\left( \frac{\partial^{2}\text{lnL}\left( \mu,\sigma \right)}{\partial\sigma^{2}} \right) = \frac{6}{\sigma^{2}} - \frac{3}{\sigma^{4}}\sum_{i = 1}^{6}{\mathrm{E}\left( \ln x_{i} - \mu \right)}^{2} = \frac{6}{\sigma^{2}} - \frac{3}{\sigma^{4}}\sum_{i = 1}^{6}{\mathrm{V}\left( \ln x_{i} \right) = \frac{6}{\sigma^{2}} - \frac{3}{\sigma^{4}}\sum_{i = 1}^{6}{\sigma^{2} = \frac{- 12}{\sigma^{2}}}}\).

Usando el negativo de estas esperanzas se obtiene la matriz de información de Fisher \[\begin{bmatrix} \frac{6}{\sigma^{2}} & 0 \\ 0 & \frac{12}{\sigma^{2}} \\ \end{bmatrix}.\]

La matriz de covarianzas, \(\Sigma\), es la inversa de la matriz de información de Fisher \[\Sigma = \begin{bmatrix} \frac{\sigma^{2}}{6} & 0 \\ 0 & \frac{\sigma^{2}}{12} \\ \end{bmatrix}.\]

La matriz estimada viene dada por \[\hat{\Sigma} = \begin{bmatrix} 0,8533 & 0 \\ 0 & 0,4267 \\ \end{bmatrix}.\]

b. El intervalo de confianza al 95% para \(\mu\) viene dado por \(9,38 \pm 1,96\sqrt{0,8533} = \left( 7,57,\ 11,19 \right)\).

El intervalo de confianza al 95% para \(\sigma^{2}\) viene dado por \(5,12 \pm 1,96\sqrt{0,4267} = \left( 3,84,\ 6,40 \right)\).

c. La media de X es \(\exp\left( \mu + \frac{\sigma^{2}}{2} \right)\). Entonces, el estimador máximo verosímil de \[g\left( \mu,\sigma \right) = \exp\left( \mu + \frac{\sigma^{2}}{2} \right)\] es \[g\left( \hat{\mu},\hat{\sigma} \right) = \exp\left( \hat{\mu} + \frac{{\hat{\sigma}}^{2}}{2} \right) = 153.277.\]

Se usa el método delta para aproximar la varianza del mle \(g\left( \hat{\mu},\hat{\sigma} \right)\).

\(\frac{\partial g\left( \mu,\sigma \right)}{\partial\mu} = exp\left( \mu + \frac{\sigma^{2}}{2} \right)\) y \(\frac{\partial g\left( \mu,\sigma \right)}{\partial\sigma} = \sigma exp\left( \mu + \frac{\sigma^{2}}{2} \right)\).

Usando el método delta, la varianza aproximada de \(g\left( \hat{\mu},\hat{\sigma} \right)\) viene dada por

\[\left. \ \hat{V}\left( g\left( \hat{\mu},\hat{\sigma} \right) \right) = \begin{bmatrix} \frac{\partial g\left( \mu,\sigma \right)}{\partial\mu} & \frac{\partial g\left( \mu,\sigma \right)}{\partial\sigma} \\ \end{bmatrix}\Sigma\begin{bmatrix} \frac{\partial g\left( \mu,\sigma \right)}{\partial\mu} \\ \frac{\partial g\left( \mu,\sigma \right)}{\partial\sigma} \\ \end{bmatrix} \right|_{\mu = \hat{\mu},\sigma = \hat{\sigma}}\]

\[= \begin{bmatrix} 153.277 & 346.826 \\ \end{bmatrix}\begin{bmatrix} 0,8533 & 0 \\ 0 & 0,4267 \\ \end{bmatrix}\begin{bmatrix} 153.277 \\ 346.826 \\ \end{bmatrix} =\]71.374.380.000

El intervalo de confianza al 95% para \(\exp\left( \mu + \frac{\sigma^{2}}{2} \right)\) viene dado por

\(153.277 \pm 1,96\sqrt{71.374.380.000} = \left( - 370.356,\ 676.910 \right)\).

Dado que la media de la distribución lognormal no puede ser negativa, se debería reemplazar el límite inferior negativo en el intervalo anterior por cero.

---

Ejemplo 3.5.4. Fondo de propiedad de Wisconsin. Para ver cómo los estimadores máximo verosímiles se aplican a datos reales, volvemos a los 2010 datos de siniestros introducidos en la Sección 1.3.

El siguiente fragmento de código muestra cómo ajustar un modelo exponencial, gamma, Pareto, lognormal y GB2. Por consistencia, el código emplea el paquete VGAM de R. El acrónimo viene de Vector Generalized Linear and Additive Models; como sugiere el nombre, este paquete puede hacer mucho más que ajustar estos modelos, aunque esto es suficiente para los propósitos requeridos en este caso. La única excepción es la densidad GB2 que no es muy utilizada fuera del mundo asegurador; en cualquier caso, puede programarse esta densidad y calcular los estimadores máximo verosímiles usando el optimizador general optim.

Mostrar Solución de Ejemplo

library(VGAM)
claim_lev <- read.csv("Data/CLAIMLEVEL.csv", header = TRUE) 
claim_data <- subset(claim_lev, Year == 2010); 

# Inferencia usando una distribución GB2 – más complicado
# La función de verosimilitud de una distribución GB2 (negativo para optimización)
lik_gb2 <- function (param) {
  a_1 <- param[1]
  a_2 <- param[2]
  mu <- param[3]
  sigma <- param[4]
  yt <- (log(claim_data$Claim) - mu) / sigma
  logexpyt <- ifelse(yt > 23, yt, log(1 + exp(yt)))
  logdens <- a_1 * yt - log(sigma) - log(beta(a_1,a_2)) - 
    (a_1+a_2) * logexpyt - log(claim_data$Claim) 
  return(-sum(logdens))
}
# "optim" es una función general utilizada con propósito de minimizar
gb2_bop <- optim(c(1, 1, 0, 1), lik_gb2, method = c("L-BFGS-B"), 
                 lower = c(0.01, 0.01, -500, 0.01), 
                 upper = c(500, 500, 500, 500), hessian = TRUE)
# Gráfico no paramétrico
plot(density(log(claim_data$Claim)), main = "", xlab = "Gastos logarítmicos",
     ylim = c(0 ,0.37))
x <- seq(0, 15, by = 0.01)
#Exponencial
fit.exp <- vglm(Claim ~ 1, exponential, data = claim_data)
theta = 1 / exp(coef(fit.exp))
fexp_ex <- dgamma(exp(x), scale = exp(-coef(fit.exp)), shape = 1) * exp(x)
lines(x, fexp_ex, col = "red", lty =2)
# Inferencia asumiendo una distribución gamma
fit.gamma <- vglm(Claim ~ 1, family = gamma2, data = claim_data)
theta <- exp(coef(fit.gamma)[1]) / exp(coef(fit.gamma)[2])  # theta = mu / alpha
alpha <- exp(coef(fit.gamma)[2]) 
fgamma_ex <- dgamma(exp(x), shape = alpha, scale = theta) * exp(x)
lines(x, fgamma_ex, col = "blue", lty =3)
#Pareto
fit.pareto <- vglm(Claim ~ 1, paretoII, loc = 0, data = claim_data)
fpareto_ex <- dparetoII(exp(x), loc = 0, shape = exp(coef(fit.pareto)[2]), 
                        scale = exp(coef(fit.pareto)[1])) * exp(x)
lines(x, fpareto_ex, col = "purple")
# Lognormal
fit.LN <- vglm(Claim ~ 1, family = lognormal, data = claim_data)
flnorm_ex <- dlnorm(exp(x), mean = coef(fit.LN)[1],
                    sd = exp(coef(fit.LN)[2])) * exp(x)
lines(x, flnorm_ex, col = "lightblue")
# Densidad para GB II
gb2_density <- function (x) {
  a_1 <- gb2_bop$par[1]
  a_2 <- gb2_bop$par[2]
  mu <- gb2_bop$par[3]
  sigma <- gb2_bop$par[4]
  xt <- (log(x) - mu) / sigma
  logexpxt <- ifelse (xt > 23, yt, log(1 + exp(xt)))
  logdens <- a_1 * xt - log(sigma) - log(beta(a_1, a_2)) - 
    (a_1+a_2) * logexpxt -log(x) 
  exp(logdens)
  }
fGB2_ex = gb2_density(exp(x)) * exp(x)
lines(x, fGB2_ex, col="green")
legend("topleft", c("log(Gastos)", "Exponencial", "Gamma", "Pareto", 
                    "Lognormal", "GB2"), cex=0.8,
       lty = c(4,2,3,1,1,1), #4 is "longdash"
       col = c("black","red","blue","purple","lightblue","green"))

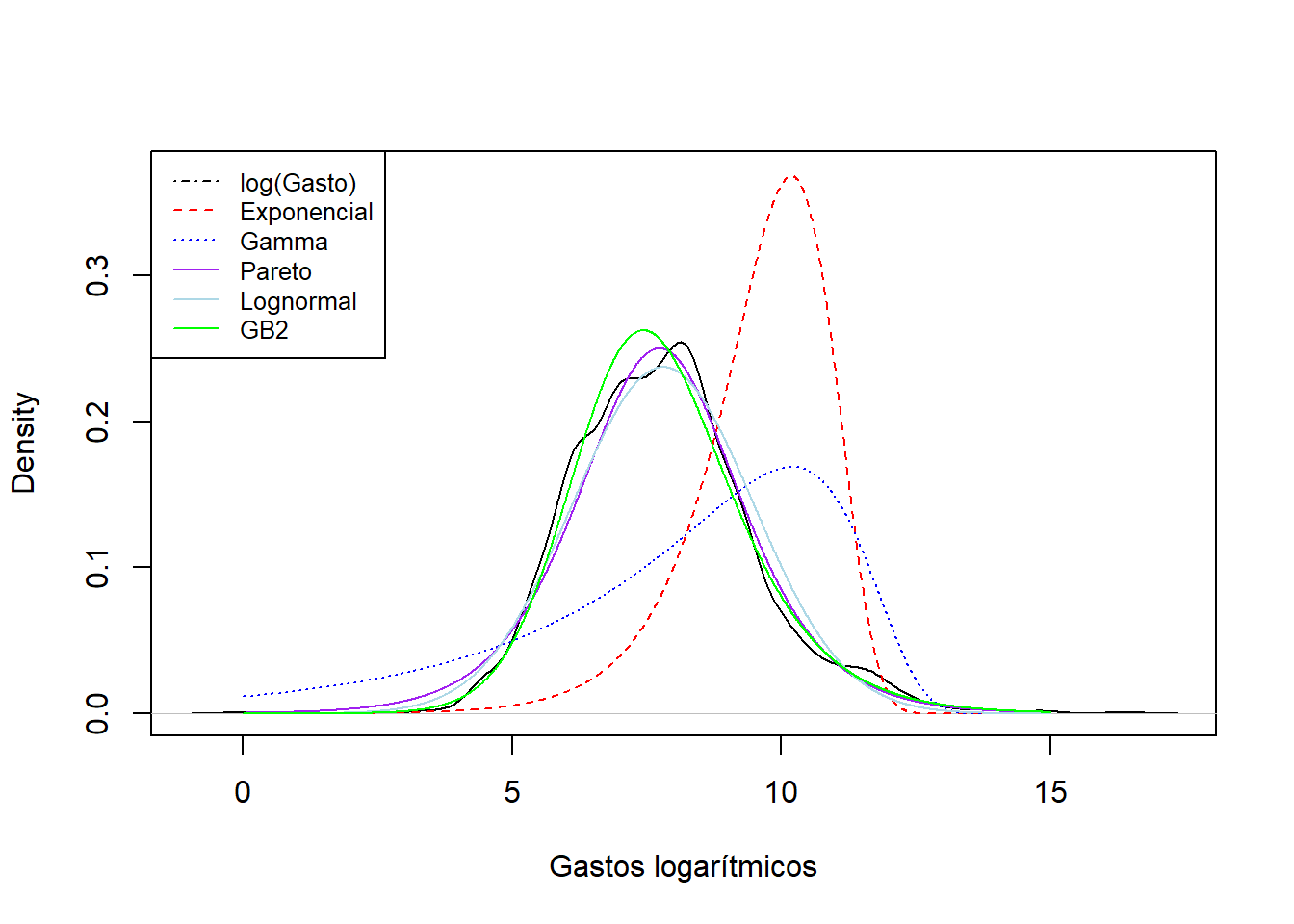
Figure 3.5: Comparaciones de densidad para el fondo de propiedad de Wisconsin

Los resultados del ejercicio de ajuste se resumen en la Figura 3.5. Aquí, la curva negra de rayas largas es un histograma suavizado para los datos reales (que introduciremos en la Sección 4.1); las otras curvas son curvas paramétricas donde los parámetros se calculan vía máxima verosimilitud. Se aprecia un pobre ajuste en la línia de rayas rojas correspondiente al ajuste de la distribución exponencial y la línea de puntos azules correspondiente al ajuste de la distribución gamma. Los ajustes de las otras curvas, Pareto, lognormal y GB2, parecen proporcionar un ajuste razonablemente bueno a los datos reales. En el Capítulo 4 se describe en más detalle los principios para la selección de modelos.

---

3.5.2 Estimadores por máxima verosimilitud usando datos modificados

En muchas aplicaciones, los actuarios y otros analistas desean estimar modelos paramétricos basados en datos individuales que no están limitados. En cualquier caso, hay también importantes aplicaciones en las que solo hay datos disponibles que están limitados o modificados. Esta sección introduce la estimación máximo verosímil para datos agrupados, censurados y truncados. Más adelante, se continuará con detalles adicionales en la Sección 4.3.

3.5.2.1 Estimadores por máxima verosimilitud para datos agrupados

En la sección anterior se consideró la estimación máximo verosímil de modelos continuos a partir de datos (individuales) completos. Cada observación individual es guardada, y su contribución a la función de verosimilitud es la densidad en ese valor. En esta sección se considera el problema de obtener estimaciones máximo verosímiles de los parámetros a partir de datos agrupados. Las observaciones están solo disponibles en forma agrupada, y la contribución de cada observación a la función de verosimilitud es la probabilidad de caer en un grupo específico (intérvalo). Sea \(n_{j}\) el número de observaciones en el intervalo \(\left( \left. \ c_{j - 1},c_{j} \right\rbrack \right.\ \) La función de verosimilitud para datos agrupados viene dada por \[ L\left( \theta \right) = \prod_{j = 1}^{k}\left\lbrack F_X\left( \left. \ c_{j} \right|\theta \right) - F_X\left( \left. \ c_{j - 1} \right|\theta \right) \right\rbrack^{n_{j}}, \] donde \(c_{0}\) es la observación más pequeña posible (a menudo establecida como cero) y \(c_{k}\) es la observación más grande posible (a menudo establecida como infinito).

Ejemplo 3.5.5. Pregunta del examen actuarial. Para un grupo de pólizas, se sabe que las pérdidas siguen la función de distribución \(F_X\left( x \right) = 1 - \frac{\theta}{x}\), para \(\theta < x < \infty.\) Además, una muestra de 20 pérdidas toma los valores:

\[ {\small \begin{matrix}\hline \text{Intervalo} & \text{Número de pérdidas} \\ \hline (\theta, 10] & 9 \\ (10, 25] & 6 \\ (25, \infty) & 5 \\ \hline \end{matrix} } \]

Calcula la estimación máximo verosímil de \(\theta\).

Mostrar Solución de Ejemplo

Solución.

La contribución de cada una de las 9 observaciones en el primer intervalo a la función de verosimilitud es la probabilidad de que \(X \leq 10\); es decir, \(\Pr\left( X \leq 10 \right) = F_X\left( 10 \right)\). De manera similar, las contribuciones de cada una de las 6 y 5 observationes en los intervalos segundo y tercero son \(\Pr\left( 10 < X \leq 25 \right) = F_X\left( 25 \right) - F_X(10)\) y \(P\left( X > 25 \right) = 1 - F_X(25)\), respectivamente. La función de verosimilitud viene dada por \[ L\left( \theta \right) = \left\lbrack F_X\left( 10 \right) \right\rbrack^{9}\left\lbrack F_X\left( 25 \right) - F_X(10) \right\rbrack^{6}\left\lbrack 1 - F_X(25) \right\rbrack^{5} \] \[ = {\left( 1 - \frac{\theta}{10} \right)}^{9}\left( \frac{\theta}{10} - \frac{\theta}{25} \right)^{6}\left( \frac{\theta}{25} \right)^{5} \] \[ = {\left( \frac{10 - \theta}{10} \right)}^{9}\left( \frac{15\theta}{250} \right)^{6}\left( \frac{\theta}{25} \right)^{5}. \] Entonces, \(\ln L \left( \theta \right) = 9\ln \left( 10 - \theta \right) + 6\ln \theta + 5\ln \theta - 9\ln 10 + 6\ln 15 - 6\ln 250 - 5\ln 25\). \[ \frac{d \ln L \left( \theta \right)}{d \theta} = \frac{- 9}{\left( 10 - \theta \right)} + \frac{6}{\theta} + \frac{5}{\theta}. \] El estimador máximo verosímil, \(\hat{\theta}\), es la solución de la ecuación \[ \frac{- 9}{\left( 10 - \hat{\theta} \right)} + \frac{11}{\hat{\theta}} = 0 \] y \(\hat{\theta} = 5,5\).

---

3.5.2.2 Estimadores por máxima verosimilitud para datos censurados

Otra posible característica distintiva de un mecanismo de recopilación de datos es la censura. Mientras que para algunos eventos de interés (pérdidas, siniestros, tiempos de vida, etc.) los datos completos pueden estar disponibles, para otros solo está disponible información parcial; todo lo que se sabe es que la observación excede un valor específico. La póliza limitada introducida en la Sección 3.4.2 es un ejemplo de censura por la derecha. Cualquier pérdida mayor o igual al límite de la póliza se iguala al límite. La contribución de la observación censurada a la función de verosimilitud es la probabilidad de que la variable aleatoria exceda el límite especificado. Nótese que las contribuciones tanto de las observaciones completas como censuradas comparten la función de supervivencia, para una observación completa esta función de supervivencia se multiplica por la función de riesgo, pero para una obseración censurada no. La función de verosimilitud para observaciones censuradas viene dada por

\[ L(\theta) = \left[ \prod_{i=1}^r f_X(x_i) \right] \left[ S_X(u) \right]^m , \] donde \(r\) es el número de cuantías de pérdidas conocidas que están por debajo del límite \(u\) y \(m\) es el número de cuantías de pérdidas mayores que el límite \(u\).

Ejemplo 3.5.6. Pregunta del examen actuarial. La variable aleatoria \(X\) tiene función de supervivencia: \[ S_{X}\left( x \right) = \frac{\theta^{4}}{\left( \theta^{2} + x^{2} \right)^{2}}. \] Sean 2 y 4 dos valores observados de \(X\). Además, otro valor excede 4. Calcula el estimador máximo verosímil de \(\theta\).

Mostrar Solución de Ejemplo

Solución.

Las contribuciones de las dos observaciones 2 y 4 son \(f_{X}\left( 2 \right)\) y \(f_{X}\left( 4 \right)\) respectivamente. La contribución de la tercera observación, de la cual solo se sabe que excede 4 es \(S_{X}\left( 4 \right)\). La función de verosimilitud viene por tanto dada por \[ L\left( \theta \right) = f_{X}\left( 2 \right)f_{X}\left( 4 \right)S_{X}\left( 4 \right). \] La función de densidad de probabilidad de \(X\) viene dada por \[ f_{X}\left( x \right) = \frac{4x\theta^{4}}{\left( \theta^{2} + x^{2} \right)^{3}}. \] Por tanto, \[ L\left( \theta \right) = \frac{8\theta^{4}}{\left( \theta^{2} + 4 \right)^{3}}\frac{16\theta^{4}}{\left( \theta^{2} + 16 \right)^{3}}\frac{\theta^{4}}{\left( \theta^{2} + 16 \right)^{2}} \\ = \frac{128\theta^{12}}{\left( \theta^{2} + 4 \right)^{3}\left( \theta^{2} + 16 \right)^{5}}, \]

Entonces, \[ \ln L\left( \theta \right) = \ln 128 + 12\ln \theta - 3\ln \left( \theta^{2} + 4 \right) - 5\ln \left( \theta^{2} + 16 \right) , \]

y

\(\frac{d \ln L\left( \theta \right)}{d \theta} = \frac{12}{\theta} - \frac{6\theta}{\left( \theta^{2} + 4 \right)} - \frac{10\theta}{\left( \theta^{2} + 16 \right)}\).

El estimador máximo verosímil, \(\hat{\theta}\), es la solución a la ecuación \[ \frac{12}{\hat{\theta}} - \frac{6\hat{\theta}}{\left( {\hat{\theta}}^{2} + 4 \right)} - \frac{10\hat{\theta}}{\left( {\hat{\theta}}^{2} + 16 \right)} = 0 \] o \[12\left( {\hat{\theta}}^{2} + 4 \right)\left( {\hat{\theta}}^{2} + 16 \right) - 6{\hat{\theta}}^{2}\left( {\hat{\theta}}^{2} + 16 \right) - 10{\hat{\theta}}^{2}\left( {\hat{\theta}}^{2} + 4 \right) = \\ - 4{\hat{\theta}}^{4} + 104{\hat{\theta}}^{2} + 768 = 0,\] que permite obtener \({\hat{\theta}}^{2} = 32\) y \(\hat{\theta} = 5,7\).

---

3.5.2.3 Estimadores por máxima verosimilitud para datos truncados

Esta sección se centra en la estimación máximo verosímil de la distribución continua de una variable aleatoria \(X\) cuando los datos estan incompletos debido a la existencia de truncamiento. Si los valores de \(X\) están truncados en \(d\), debe tenerse en cuenta que podria pasar desapercibida la existencia de estos valores si no superasen \(d\). La franquícia introducida en la póliza en la Sección 3.4.1 es un ejemplo de truncamiento por la izquierda. Cualquier pérdida menor o igual a la franquícia no se registra. La contribución a la función de verosimilitud de una observación \(x\) truncada en \(d\) será una probabilidad condicionada y \(f_{X}\left( x \right)\) será reemplazado por \(\frac{f_{X}\left( x \right)}{S_{X}\left( d \right)}\). La función de verosimilitud para datos truncados viene dada por

\[ L(\theta) = \prod_{i=1}^k \frac{f_X(x_i)}{S_X(d)} , \] donde \(k\) es el número de cuantías de pérdidas mayores que la franquicia \(d\).

Ejemplo 3.5.7. Pregunta del examen actuarial. Para una distribución de Pareto de un solo parámetro con \(\theta = 2\), se aplica la estimación máximo verosímil para estimar el parámetro \(\alpha\). Determina la media estimada de la distribución ground up loss en base a la estimación máximo verosímil de \(\alpha\) para la siguiente base de datos:

• Franquicia ordinaria en la póliza de 5, máxima pérdida cubierta de 25 (límite de la póliza 20)
• 8 cuantías de seguro pagadas: 2, 4, 5, 5, 8, 10, 12, 15
• 2 límites de pago: 20, 20.

Mostrar Solución de Ejemplo

Solución.

Las contribuciones de las diferentes observaciones pueden ser resumidas a continuación:

• Para la pérdida exacta: \(f_{X}\left( x \right)\)
• Para las observaciones censuradas: \(S_{X}\left( 25 \right)\).
• Para las observaciones truncadas: \(\frac{f_{X}\left( x \right)}{S_{X}\left( 5 \right)}\).

Dado que las ground up losses menores de 5 se omiten del conjunto de datos, la contribución de todas las observaciones debe estar condicionada a exceder 5. La función de verosimilitud resulta ser \[ L\left( \alpha \right) = \frac{\prod_{i = 1}^{8}{f_{X}\left( x_{i} \right)}}{\left\lbrack S_{X}\left( 5 \right) \right\rbrack^{8}}\left\lbrack \frac{S_{X}\left( 25 \right)}{S_{X}\left( 5 \right)} \right\rbrack^{2}. \] Para la Pareto de un parámetro las funciones densidad de probabilidad y distribución vienen dadas por

\[ f_{X}\left( x \right) = \frac{\alpha\theta^{\alpha}}{x^{\alpha + 1}} \ \ \text{and} \ \ F_{X}\left( x \right) = 1 - \left( \frac{\theta}{x} \right)^{\alpha}, \] para \(x > \theta\), respectivamente. Entonces, la función de verosimilitud y el logaritmo de la función de verosimilitud vienen dadas por \[ L\left( \alpha \right) = \frac{\alpha^{8}}{\prod_{i = 1}^{8}x_{i}^{\alpha + 1}}\frac{5^{10\alpha}}{25^{2\alpha}}, \] \[ \ln L \left( \alpha \right) = 8\ln\alpha - \left( \alpha + 1 \right)\sum_{i = 1}^{8}{\ln x_{i}} + 10\alpha \ln 5 - 2\alpha \ln 25. \]

\(\frac{d \ln L \left( \alpha \right)}{d \theta} = \frac{8}{\alpha} - \sum_{i = 1}^{8}{\ln x_{i}} + 10\ln 5 - 2\ln 25\).

El estimador máximo verosímil, \(\hat{\alpha}\), es la solución de la ecuación \[ \frac{8}{\hat{\alpha}} - \sum_{i = 1}^{8}{\ln x_{i}} + 10\ln 5 - 2\ln 25 = 0, \] que resulta en \[ \hat{\alpha} = \frac{8}{\sum_{i = 1}^{8}{\ln x_{i}} - 10\ln 5 + 2\ln 25} = \frac{8}{(\ln 7 + \ln 9 + \cdots + \ln 20) - 10\ln 5 + 2\ln 25} = 0,785. \] La media de la Pareto solo existe para \(\alpha > 1\). Dado que \(\hat{\alpha} = 0,785 < 1\). Entonces, la media no existe.

---

3.6 Recursos y Contribuciones Adicionales

Colaboradores

• Zeinab Amin, The American University in Cairo, es el principal autor de este capítulo. Email: zeinabha@aucegypt.edu para comentarios sobre el capítulo y sugerencias de mejora.
• Numerosos comentarios de gran utilidad han sido proporcionados por Hirokazu (Iwahiro) Iwasawa, iwahiro@bb.mbn.or.jp .
• Otros revisores del capítulo son: Rob Erhardt, Jorge Yslas, Tatjana Miljkovic, y Samuel Kolins.
• Traducción al español: Ana Maria Pérez-Marín (Universitat de Barcelona)

Ejercicios

Se proporciona una lista de ejercicios que sirven de guía al lector sobre algunos de los fundamentos teóricos de ** Loss Data Analytics **. Cada tutorial se basa en una o más preguntas de los examenes para la profesión actuarial – típicamente el Examen C de la Sociedad de Actuarios.

Severity Distribution Guided Tutorials

Lecturas y referencias adicionales

Notables contribuciones incluyen a: Cummins and Derrig (2012), Frees and Valdez (2008), Klugman, Panjer, and Willmot (2012), Kreer et al. (2015), McDonald (1984), McDonald and Xu (1995), Tevet (2016), and Venter (1983).

Bibliography

Cummins, J. David, and Richard A. Derrig. 2012. Managing the Insolvency Risk of Insurance Companies: Proceedings of the Second International Conference on Insurance Solvency. Vol. 12. Springer Science & Business Media.

Frees, Edward W., and Emiliano A. Valdez. 1998. “Understanding Relationships Using Copulas.” North American Actuarial Journal 2 (01): 1–25.

2008. “Hierarchical Insurance Claims Modeling.” Journal of the American Statistical Association 103 (484): 1457–69.

Klugman, Stuart A., Harry H. Panjer, and Gordon E. Willmot. 2012. Loss Models: From Data to Decisions. John Wiley & Sons.

Kreer, Markus, Ayşe Kızılersü, Anthony W Thomas, and Alfredo D Egı́dio dos Reis. 2015. “Goodness-of-Fit Tests and Applications for Left-Truncated Weibull Distributions to Non-Life Insurance.” European Actuarial Journal 5 (1): 139–63.

McDonald, James B. 1984. “Some Generalized Functions for the Size Distribution of Income.” Econometrica: Journal of the Econometric Society, 647–63.

McDonald, James B, and Yexiao J Xu. 1995. “A Generalization of the Beta Distribution with Applications.” Journal of Econometrics 66 (1-2): 133–52.

Tevet, Dan. 2016. “Applying Generalized Linear Models to Insurance Data.” Predictive Modeling Applications in Actuarial Science: Volume 2, Case Studies in Insurance, 39.

Venter, Gary. 1983. “Transformed Beta and Gamma Distributions and Aggregate Losses.” In Proceedings of the Casualty Actuarial Society, 70:289–308. 133 & 134.